Definition - Konvergenz einer Folge

• Typen:
  • Konvergenz einer Funktion
  • Reihenkonvergenz
  • Punktweise Konvergenz
  • Stochastische Konvergenz
  • Konvergenz im p-ten Mittel
  • Fast-sichere Konvergenz
• Beispiele:
  • Beispiel - Die konstante Folge
  • Beispiel - Die konvergierende Exponenten-Folge
  • Lemma - Die Folge der rationalen Exponenten
  • Proposition - Folge reeller Exponenten
  • Grenzwertverhalten der Potenzfunktion
  • n)
  • Brüche
    • Die Folge (folgt aus dem Satz des Eudoxos)
    • Aufgabe - Die Folge (frac{1}{2n+1})
    • Aufgabe - Die Folge (frac{1}{2^{n-1}}
    • Aufgabe - Die Folge ((-1) hoch n frac{17}{n}
    • Aufgabe - Die Folge (1+frac{1}{2n-1})
    • Aufgabe - Die Folge (-1+frac{1}{2n})
    • Beispiel - Die konvergente Summenbruch-Folge
    • Proposition - Nullfolge in Exponentialfunktion und Bruch
  • Wurzeln
    • Beispiel - Die Wurzelbruch-Folge
    • Beispiel - Die Wurzelfolge
    • Proposition - Die Wurzelfolge einer Konstanten
    • Beispiel - Die Wurzel einer Folge
  • Euler’sche Zahl
    • Beispiel - Die e-Folge
    • Proposition - (1+frac{1}{n}) hoch n konvergiert gegen die Euler’sche Zahl
    • Proposition - Die Folge die gegen 1 durch e konvergiert
    • Beispiel - Die konvergente Summenbruch-Folge mit Fakultät
• Konstrukte:
  • Grenzwert
  • Divergenz
  • Nullfolge
  • Euler’sche Zahl
  • Häufungspunkt
  • Reihenkonvergenz
• Eigenschaften:
  • Der Grenzwert von (a_n-a)=0
  • Teilfolgen konvergieren gegen denselben Grenzwert
  • Jede konvergente Folge ist beschränkt
  • Proposition - Eine Folge konvergiert nicht gegen a iff eine Teilfolge liegt vollständig außerhalb einer Epsilon-Umgebung
  • Grenzwert-Vergleichssatz
  • Grenzwert-Verhalten und Ungleichung
  • Betragssatz
  • Multiplikation mit Nullfolgen
  • Rechenregeln konvergenter Folgen
  • Potenzrechenregel konvergenter Folgen
  • Logarithmus einer konvergenten Folge positiver reeller Zahlen
• Hinreichende Aussagen:
  • Einschnürungssatz
  • Monotonieprinzip
  • Auswahlprinzip von Bolzano-Weierstraß
  • Theorem - Folge konvergiert gdw Folge ist Cauchyfolge
  • Ausnutzen der Rechenregeln konvergenter Folgen
• Charakterisierungen:
  • Korollar - Monotone Folge konvergiert gdw Monotone Folge ist beschränkt
  • Cauchyfolge (siehe Korollar 13.5.17)
• Involvierte Definitionen:
  • Folge
  • Epsilon-Umgebung
• Referenz: Mathegrundlagen

Definition: Konvergenz einer Folge

Eine Folge konvergiert gegen

• (Definition 13.1.6) wenn in jeder -Umgebung fast alle Glieder von liegen oder
• (Definition 13.1.8) wenn

Wobei die Punkte im Ergebnis äquivalent sind.

Anmerkungen

Also: jede 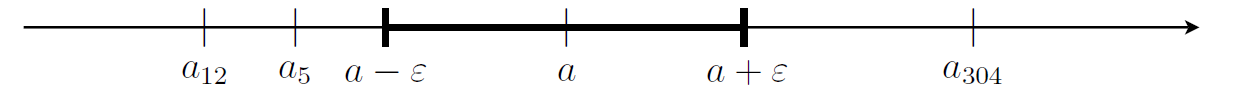-Umgebung (hier fett) von enthält fast alle :

Wie man prüfen kann, ob eine Folge konvergiert:

Wähle beliebig. Zeige, dass es ein gibt, sodass .