Theorem - Epsilon-Delta-Kriterium für Stetigkeit

• Bewiesen durch:
  • Proposition 15.1.8
  • Bemerkung 12.2.20
• Involvierte Definitionen:
  • Stetigkeit
  • Funktion
• Referenz: Mathegrundlagen

⠀

Theorem: Epsilon-Delta-Kriterium für Stetigkeit

Sei eine Funktion.

Dann gilt: ist stetig in

Anmerkung

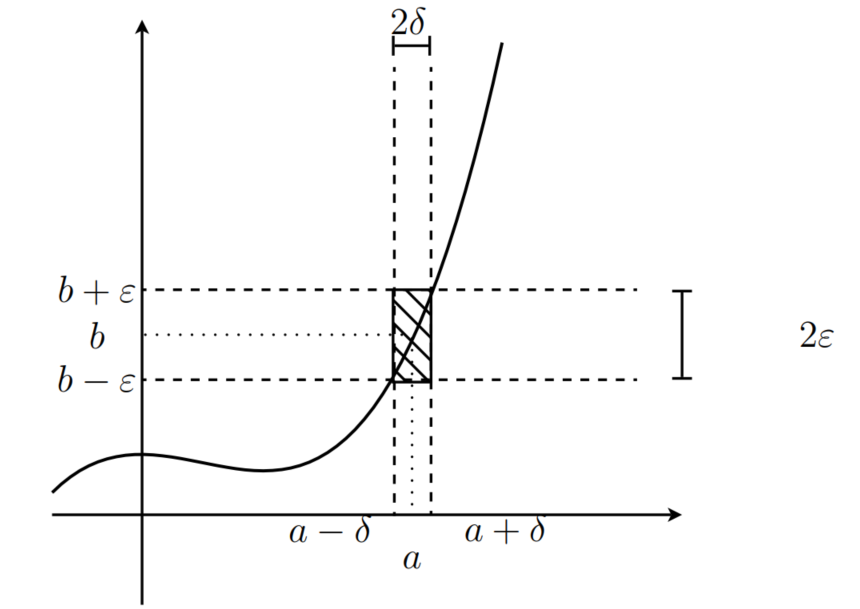
Visualisierung des --Kriteriums

Beweis

Teil 1:

Sei in stetig und sei .

Dann gilt:

Mit Proposition 15.1.8 gibt es eine -Umgebung , sodass

Dabei gilt mit Bemerkung 12.2.20:

Mit Gleichungen und erhalten wir also:

Wieder mit Bemerkung 12.2.20 ist Gleichung äquivalent zu

was zu zeigen war.

Teil 2:

Wir nehmen an, das --Kriterium sei erfüllt. Sei hierzu eine Folge, die gegen konvergiert.
Sei außerdem .

Nach Definition 15.1.1 ist zu zeigen, dass

Wir wählen nun so, dass

(also so, dass es den letzten Teil des --Kriterium erfüllt).

Da gilt mit Definition 13.1.8:

Damit erfüllen also alle mit die Implikation aus Gleichung und mit Definition 13.1.8 gilt:

was zu zeigen war.