Proposition - Stetigkeit und Delta-Umgebung

• Involvierte Definitionen:
  • Stetigkeit
  • Epsilon-Umgebung
• Referenz: Mathegrundlagen

⠀

Proposition: Stetigkeit und Delta-Umgebung

Sei stetig in .
Sei insbesondere .

Dann gibt es eine -Umgebung , sodass

Anmerkung

TIP

Es gilt:

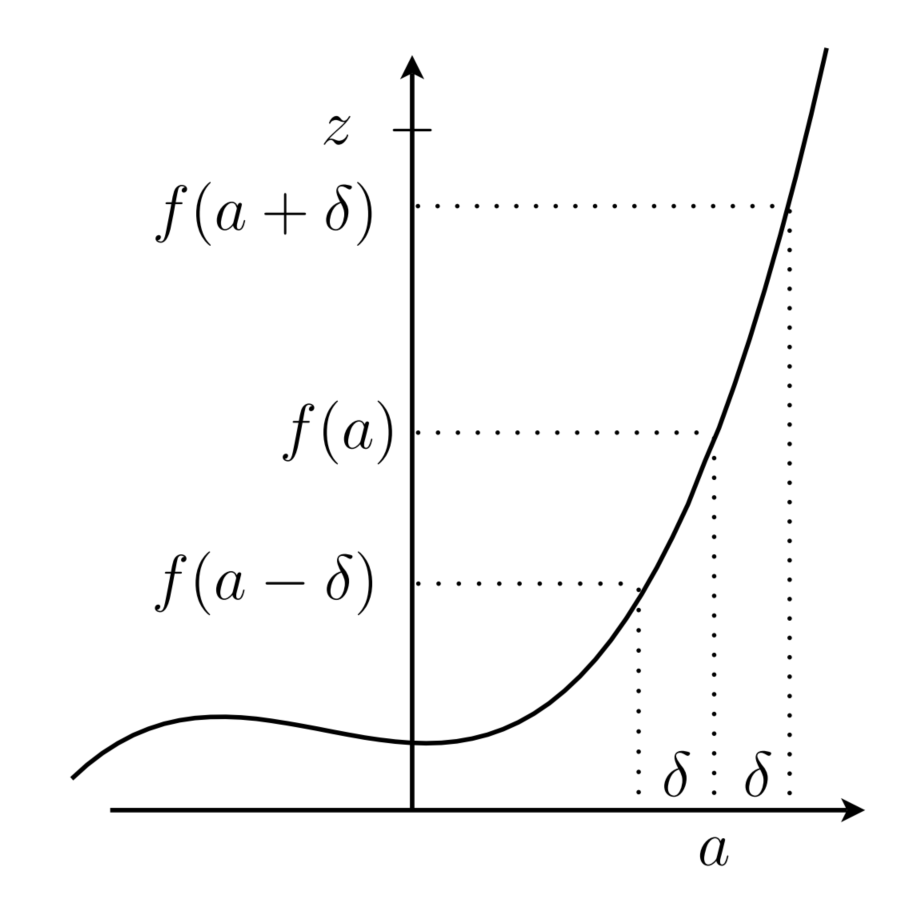
Visualisierung

Beweis

Wir führen den Beweis durch Widerspruch. Angenommen, eine solche -Umgebung würde nicht existieren.

Das würde bedeuten, dass es für jedes mögliche ein gibt, sodass oder . Ganz formell wäre die Aussage dann:

Die Fälle mit , sind dabei natürlich inbegriffen. Mit Gleichung gilt also auch:

Da , schnürt sich die Umgebung immer weiter um zu. Entsprechend konvergiert gegen .

Da, wie vorausgesetzt, in stetig ist, gilt mit Definition 15.1.1, dass

Wir hatten vorausgesetzt, dass

gilt. Für alle gilt mit jedoch

Entsprechend kann auch nicht gelten ↯. Das ist ein Widerspruch zu der Annahme . Mit diesem Widerspruch gilt die Aussage.