Konstrukte:Generalisierungen:Eigenschaften:Charakterisierungen:Involvierte Definitionen:
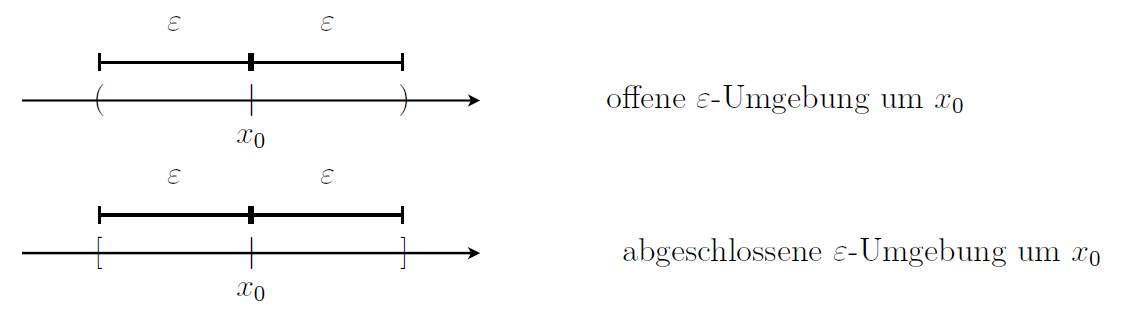
Definition: Epsilon-Umgebung
Sei
beziehungsweise ein Intervall. Sei der Mittelpunkt. Und sei der Radius. Dann nennen wir
offene -Umgebung und abgeschlossene -Umgebung.
Anmerkung
Offene
-Umgebungen = -Umgebung Da offene
-Umgebungen häufiger betrachtet werden als abgeschlossene, bezeichnet man sie in der Regel einfach nur als -Umgebung.
Anschaulich: Wenn wir um
Das sind die Randpunkte des Intervalls.
Die Punkte, die auf der Zahlengerade zwischen diesen beiden Randpunkten liegen, sind genau die Punkte der
Visuell: