Definition - Lokales Minimum einer Funktion

• Generalisierungen:
  • Lokales Extremum
• Eigenschaften:
  • Unterscheidung von Maximum und Minimum über die zweite Ableitung
  • Lokales Minimum konvexer Funktion ist auch globales Minimum
• Notwendige Aussagen:
  • Ableitung in einem lokalen Extremum ist Null
• Hinreichende Aussagen:
  • Proposition - Zweite Ableitung ist ungleich Null gdw Funktion hat lokales Extremum
  • Gradientenabstiegsverfahren (kann aber auch lediglich zu einem Sattelpunkt führen …)
  • Newton-Verfahren für Minimierungsprobleme (kann auch zu einem Sattelpunkt führen …)
• Involvierte Definitionen:
  • Funktion
  • Delta-Umgebung
  • Offene Kugel
• Referenz: Mathegrundlagen

⠀

Definition: Lokales Minimum einer Funktion

Sei ein Punkt.
Sei eine Funktion.

Wir sagen, dass in ein lokales Minimum besitzt, wenn es eine -Umgebung so gibt, dass

gilt.

In diesem Fall bezeichnen wir als lokales Minimum.

Definition: Lokales Minimum einer mehrdimensionalen Funktion

Sei eine Menge.
Sei eine Funktion.

Wir sagen, dass in ein lokales Minimum besitzt, wenn es eine offene Kugel mit so gibt, dass

gilt.

In diesem Fall bezeichnen wir als lokales Minimum.

Anmerkung

Achtung:

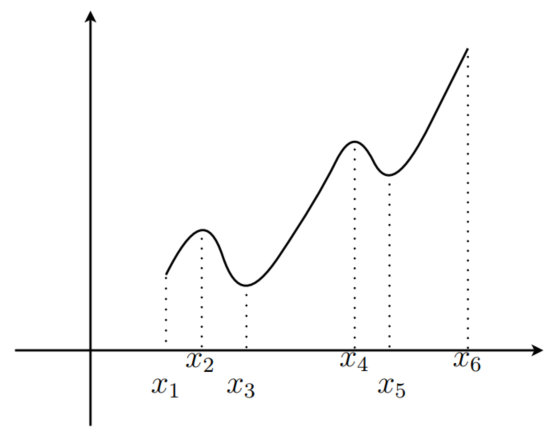
Eine Funktion kann viele lokale Extrema haben: