Theorem - Nullstellensatz von Bolzano

• Bewiesen durch:
  • Supremumsprinzip
  • Lemma 15.2.1 2.)
  • Proposition 15.1.8
• Involvierte Definitionen:
  • Stetigkeit
  • Funktion
  • Nullstelle
• Referenz: Mathegrundlagen

⠀

Theorem: Nullstellensatz von Bolzano

Sei eine stetige Funktion mit

• (oder vice versa)

Dann gilt:

Das heißt: in dem offenen Intervall gibt es mindestens eine Nullstelle von .

Anmerkung

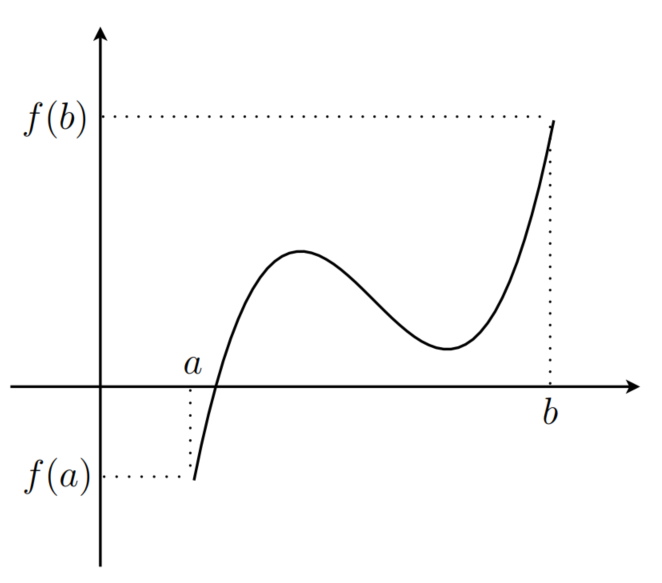
Visualisierung

Die Funktion muss die x-Achse schneiden, wenn sie auf einem Intervallende größer als und auf dem anderen kleiner als ist:

Beweis

Sei o.b.d.A. und .

Sei die Menge der Urbilder, deren Bild unter kleiner/gleich ist, also:

Von wissen wir bereits:

• ist nicht leer, denn gilt ja auf jeden Fall und damit .
• ist beschränkt. Da ist auf jeden Fall eine obere Schranke von .

Daher gilt mit dem Supremumsprinzip, dass ein Supremum besitzt.

Mit Lemma 15.2.1 2.) gibt es eine Folge mit und

Da nach Voraussetzung stetig ist, gilt:

und da wegen für alle gilt, dass , gilt auch

Wir zeigen jetzt nun, dass sogar gilt: . Angenommen, . Dann gibt es mit Proposition 15.1.8 ein , sodass

Es gäbe dann also noch Punkte, die größer als sind, aber für die trotzdem . Das ist jedoch ein Widerspruch zu der Annahme, dass das Supremum ist.

Es folgt, dass also , was zu zeigen war.