Proposition: Vergleichssatz

Seien zwei Folgen mit

und

.

Gilt für fast alle Glieder , dann folgt:

Beweis

Wir führen den Beweis durch Widerspruch. Dafür nehmen wir an, dass .

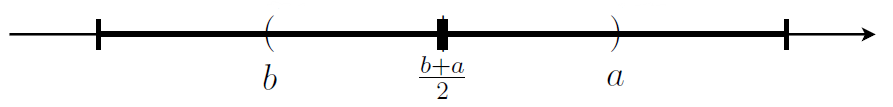
Wir betrachten nun das offene Intervall . Nach Definition ist der Mittelpunkt und der Radius :

Jetzt platzieren wir hier noch die beiden -Umgebungen für :

Da der Grenzwert für ist, müssen fast alle Glieder von in liegen.

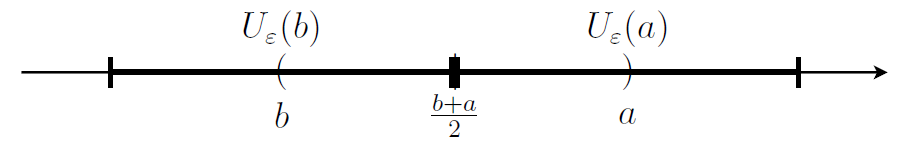
Dann gilt aber für fast alle Glieder von und , dass . Das ist ein Widerspruch zu der Voraussetzung, dass für fast alle Glieder .

Es folgt, dass gelten muss.

/vault