Definition - Zufallsvariable

• Typen:
  • Numerische Zufallsvariable
  • Reelle Zufallsvariable
    • Diskrete Zufallsvariable
    • Stetige Zufallsvariable
  • Zufallsvektor
  • Folge unabhängiger Zufallsvariablen
  • Projektionsabbildung
  • Folge von Zufallsvariablen
  • Statistik (Funktion)
  • Hypothese (ML)
• Beispiele:
  • Indikatorfunktion von Ereignissen
• Konstrukte:
  • Realisierung einer Zufallsvariablen
  • Verteilung einer Zufallsvariablen
  • Wahrscheinlichkeitsraum einer Zufallsvariablen
  • Moment
    • Erwartungswert
  • Zentrales Moment
    • Varianz
    • Standardabweichung
  • Kovarianz
  • Korrelationskoeffizient
  • Induziertes Wahrscheinlichkeitsmaß
  • Mengenschreibweise bei Zufallsvariablen
  • Stochastische Unabhängigkeit von Zufallsvariablen
  • Unkorreliertheit von Zufallsvariablen
• Generalisierungen:
  • Zufallsvektor
  • Messbare Abbildung
• Eigenschaften:
  • Cauchy-Schwarz-Ungleichung für Zufallsvariablen
  • Chernoff-Schranke für die Summe stochastisch unabhängiger Zufallsvariablen
• Involvierte Definitionen:
  • Urbildabbildung
  • Wahrscheinlichkeitsraum
  • Messbare Abbildung
  • vgl. auch Statistik (Funktion)
• Veranstaltung: AlMa, EiS
• Referenz: } AlgoMathe KE1 - Zufallsvariablen, @henze2019

⠀

Definition: Zufallsvariable

Seien zwei Grundmengen.
Seien , zwei -Algebren.

Wir bezeichnen als -wertige Zufallsvariable, falls gilt:

ist eine -messbare Abbildung.

Anmerkung

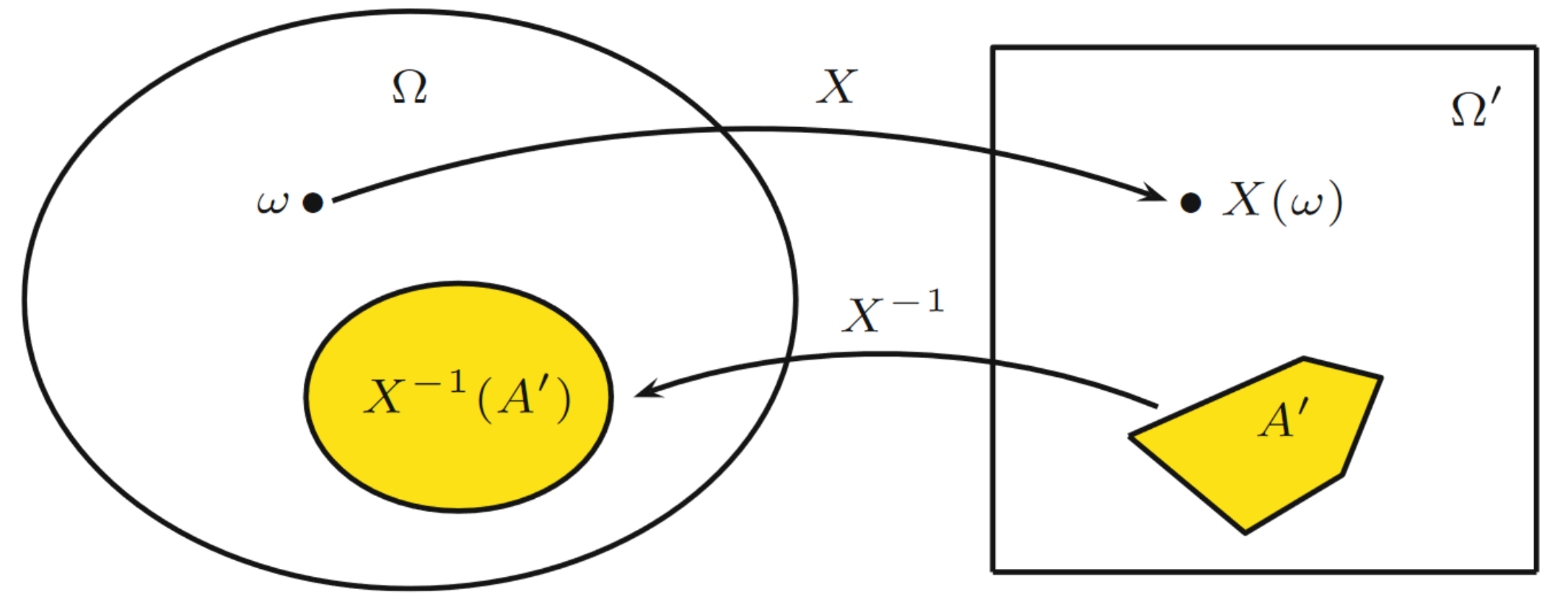
Darstellung einer Zufallsvariable mit zugehöriger Urbildabbildung ¹:

Merke:

Auch die Addition zweier Zufallsvariablen ist wieder eine Zufallsvariable:

Seien Zufallsvariablen und So ist

Interpretation

Zufallsvariablen sind also bloß Funktionen, die von einem Grundraum in einen anderen Grundraum abbilden.

Ob surjektiv oder injektiv ist, ist egal.
Wichtig ist nur, dass es sich bei den Urbildern der Ereignisse auch wirklich um Ereignisse in handelt.

Denn da , wäre es ja auch denkbar, dass zwar , aber .

Andernfalls wäre nicht strukturverträglich