Definition - Konvexe Menge

• Beispiele:
  • Jeder Untervektorraum von
  • Affiner Raum
  • Offene Kugel
  • Abgeschlossene Kugel
  • Menge dualer Variablen ist konvex
• Konstrukte:
  • Konvexe Funktion
  • Relatives Inneres
• Generalisierungen:
  • Menge
  • Affiner Raum?
• Eigenschaften:
  • Durchschnitt konvexer Mengen ist konvex
  • Summe konvexer Mengen ist konvex
  • Kartesisches Produkt konvexer Mengen ist konvex
• Involvierte Definitionen:
  • Vektorraum
  • Teilmenge
  • Abgeschlossenes Intervall
  • siehe auch Nicht-konvexe Menge
• Veranstaltung: MatheDS
• Referenz: @riedel2023

⠀

Definition: Konvexe Menge

Sei ein -dimensionaler Vektorraum.

Wir bezeichnen als konvex, wenn:

wenn also jeder Punkt auf der Verbindungslinie zwischen und wieder in liegt.

Konvexkombination

Den Term bezeichnet man auch als Konvexkombination.

Anmerkung

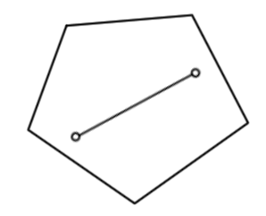
Beispiele für konvexe Figuren in

Hier zwei Beispiele für konvexe Figuren in .

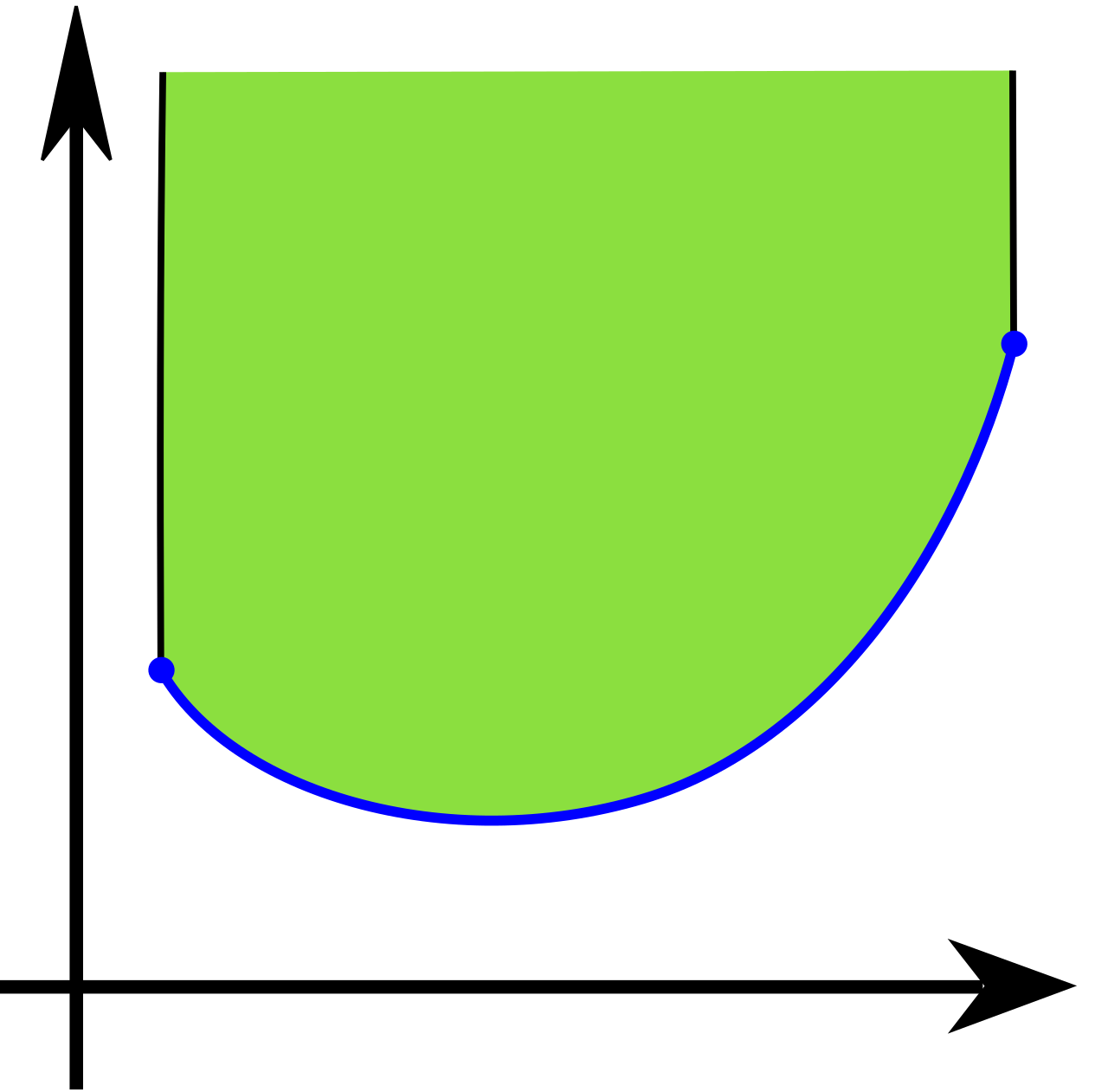
Als besonderes Beispiel hier eine konvexe Menge über dem Graphen einer Funktion:

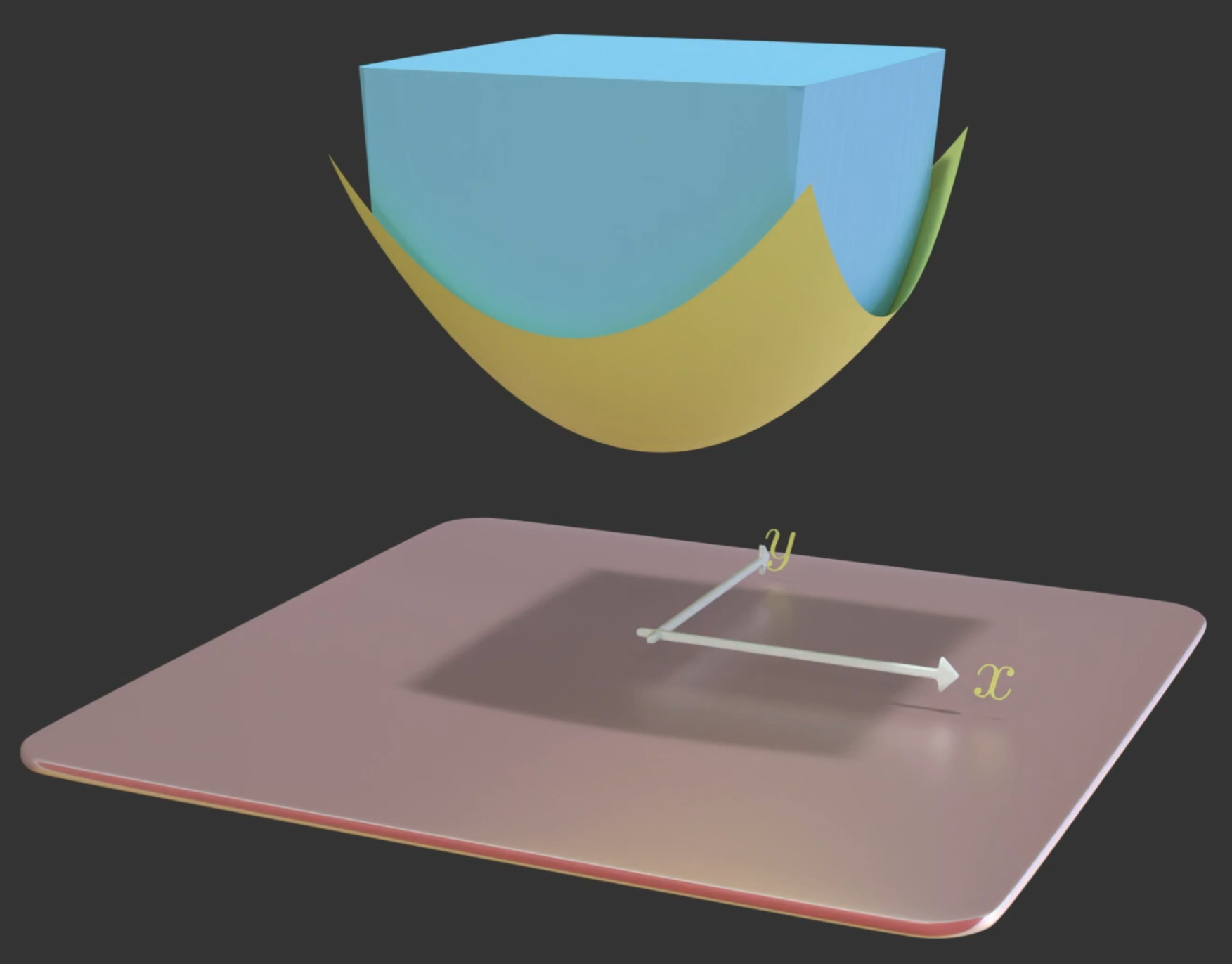
oder im dreidimensionalen:

¹

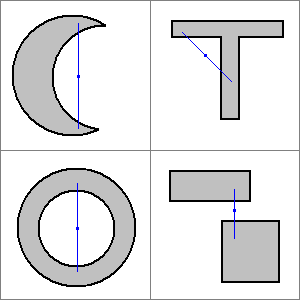
Beispiele für konkave (nichtkonvexe) Mengen in

²

Footnotes

1. Siehe https://youtube.com/watch?v=d0CF3d5aEGc ↩

2. Siehe https://de.wikipedia.org/wiki/Konvexe_Menge#/media/Datei:KonkaveFiguren.png ↩