Definition - Konvexe Funktion

• Typen:
  • Strikt konvexe Funktion
  • μ-stark konvexe Funktion
• Beispiele:
  • Norm
  • Maximum
  • Softmax
  • LogSumExp
  • Lineare Abbildung
• Konstrukte:
  • Konvexes Optimierungsproblem
• Generalisierungen:
  • Funktion
  • Stetige Funktion
• Eigenschaften:
  • Jensensche Ungleichung für den Erwartungswert
  • Konvexe Funktionen sind stetig
  • Addition konvexer Funktionen ist konvex
  • Skalarmultiplikation mit konvexer Funktion ist konvex
  • Lokales Minimum konvexer Funktion ist auch globales Minimum
  • Konvexe Funktion hat ihr globales Minimum an der Stelle, an der der Gradient null ist
  • Gradientenabstiegsverfahren konvergiert für L-glatte und konvexe Funktionen Funktionen
• Hinreichende Bedingungen:
  • Funktion ist konvex ist konkav.
  • h konvex und monoton wachsend und g konvex ⇒ h(g) konvex
  • h konvex und monoton fallend und g konkav ⇒ h(g) konvex
  • h konkav und monoton wachsend und g konkav ⇒ h(g) konkav
  • h konkav und monoton fallend und g konvex ⇒ h(g) konkav
• Charakterisierungen:
  • Funktion ist konvex Epigraph (die Fläche über dem Funktionsgraphen) ist konvex.
  • Funktion ist konvex gdw
  • Funktion ist konvex gdw Hessematrix ist positiv semidefinit
• Involvierte Definitionen:
  • Konvexe Menge
  • Funktion
  • Abgeschlossenes Intervall
  • Sekante
  • Siehe auch Konkave Funktion
• Veranstaltung: MatheDS
• Referenz: @riedel2023

⠀

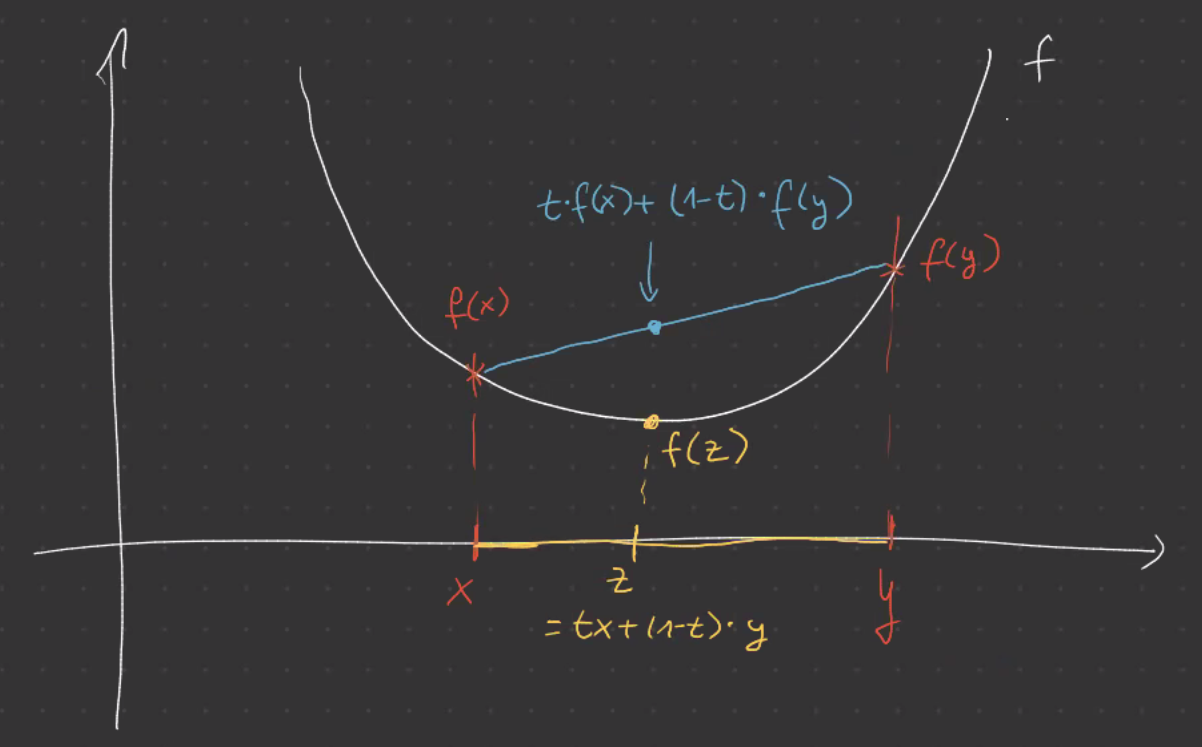
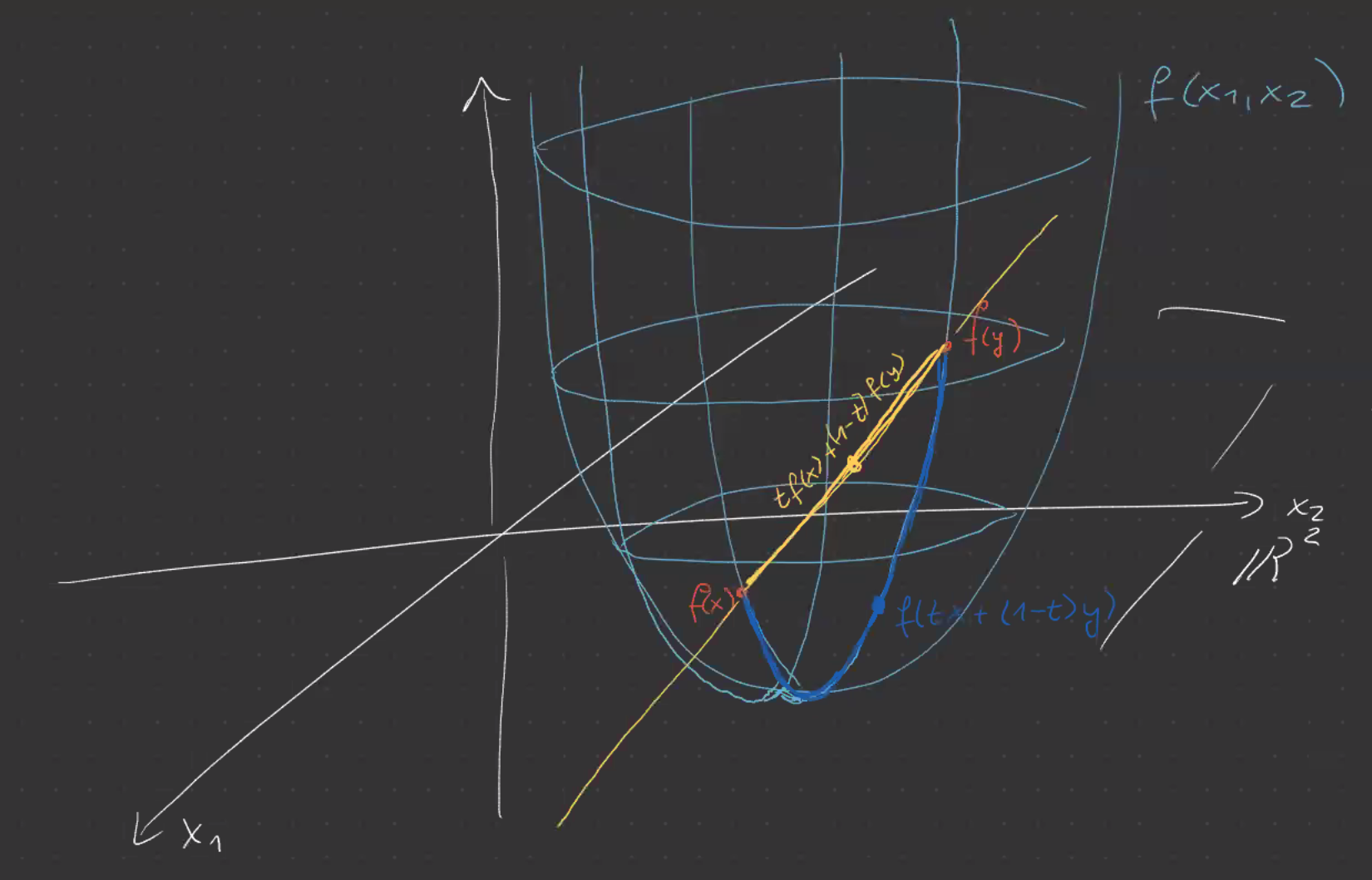
Definition: Konvexe Funktion

Sei eine konvexe Menge.
Sei eine Funktion.

Wir bezeichnen als konvex, wenn

Das heißt, wenn die Sekante durch die zwei Punkte und im Bereich zwischen diesen beiden Punkten auf oder oberhalb des Funktionsgraphen von liegt.

Anmerkung

Und wie sieht so eine konvexe Funktion jetzt aus?

Eine konvexe Funktion macht auf dem Intervall eine “Linkskurve” in Richtung wachsender -Werte. Anschaulich:

¹

Insbesondere gilt im zweidimensionalen:

²

sowie im dreidimensionalen:

²

Und weshalb ist hier jetzt in dem offenen Intervall?

Das offene Intervall wird insbesondere für die Definition strikt konvexer Funktionen benötigt.

Footnotes

1. @teschl2014 ↩

2. Tutorium von Dr. Leonie Brinker ↩ ↩²