Definition - Normalverteilung

• Typen:
  • Standardnormalverteilung
• Konstrukte:
  • Gaußsches Produktmodell
  • Denoising Autoencoder
• Generalisierungen:
  • Mehrdimensionale Normalverteilung
  • Standardnormalverteilung
  • Dichte einer stetigen Zufallsvariable
  • Absolut stetige Verteilungsfunktion einer Zufallsvariablen
  • Exponentialfamilie
• Eigenschaften:
  • Additionsgesetz der Normalverteilung
  • Stauchen und Verschieben der Normalverteilung
  • Studentisierung von Realisierungen normalverteilter Zufallsvariablen
  • Standardabweichungen vom Mittelwert einer Normalverteilung
• Hinreichende Bedingungen:
  • Komponenten der mehrdimensionalen Normalverteilung sind normalverteilt
• Involvierte Definitionen:
  • Erwartungswert
  • Varianz
  • Stetige Zufallsvariable
  • Dichte
  • Absolut stetige Verteilungsfunktion einer Zufallsvariablen
• Veranstaltung: EiS
• Referenz: @henze2019

⠀

Definition: Dichte der Normalverteilung

Sei der Erwartungswert.
Sei die Varianz.

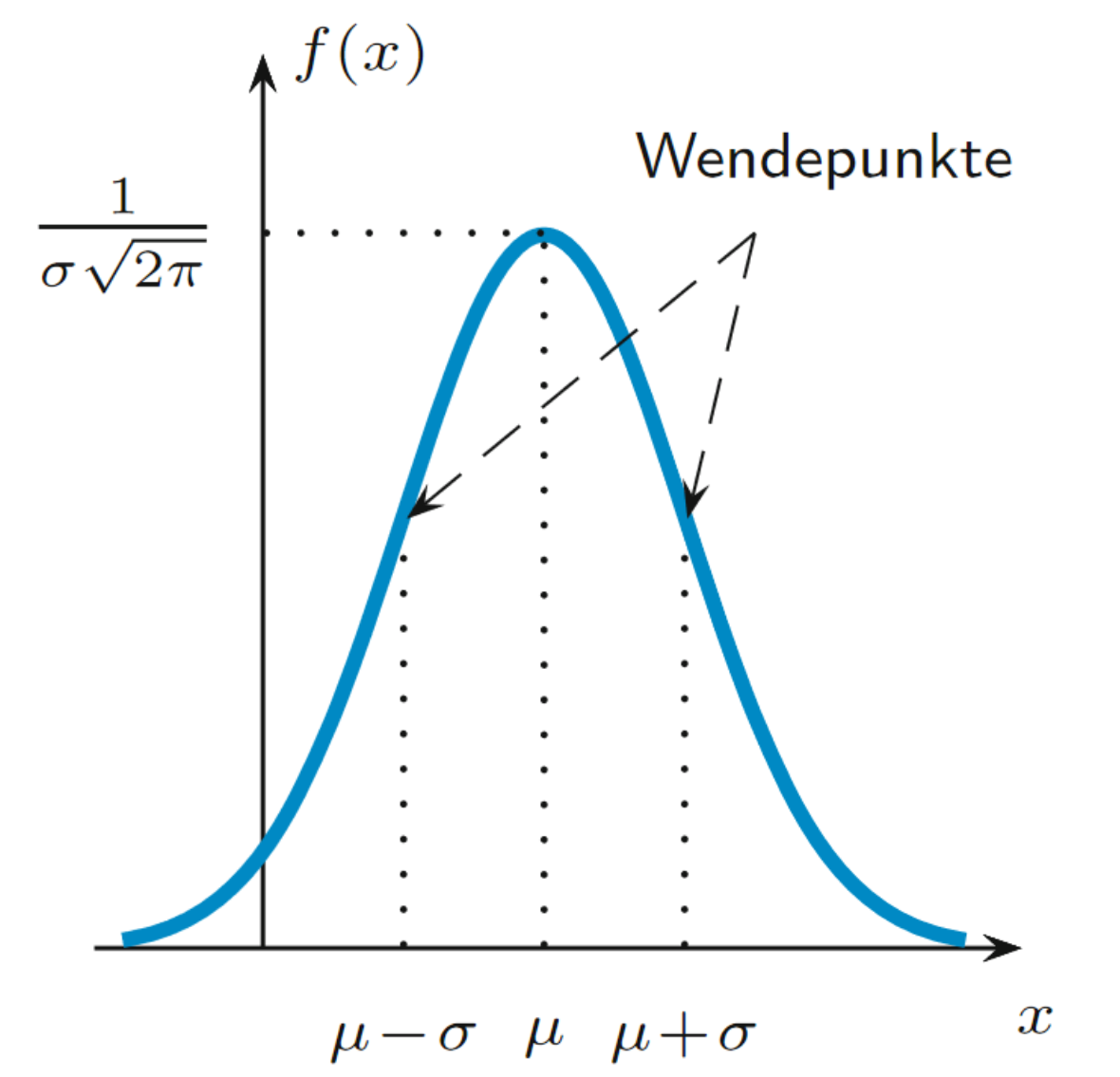
Wir bezeichnen die Zufallsvariable als normalverteilt , wenn die folgende Dichte besitzt:

Folgende Abbildung zeigt die Dichte der Normalverteilung¹

Definition: Verteilungsfunktion der Normalverteilung

Sei eine normalverteilte Zufallsvariable.

In Anlehnung an die Verteilungsfunktion der Standardnormalverteilung setzen wir:

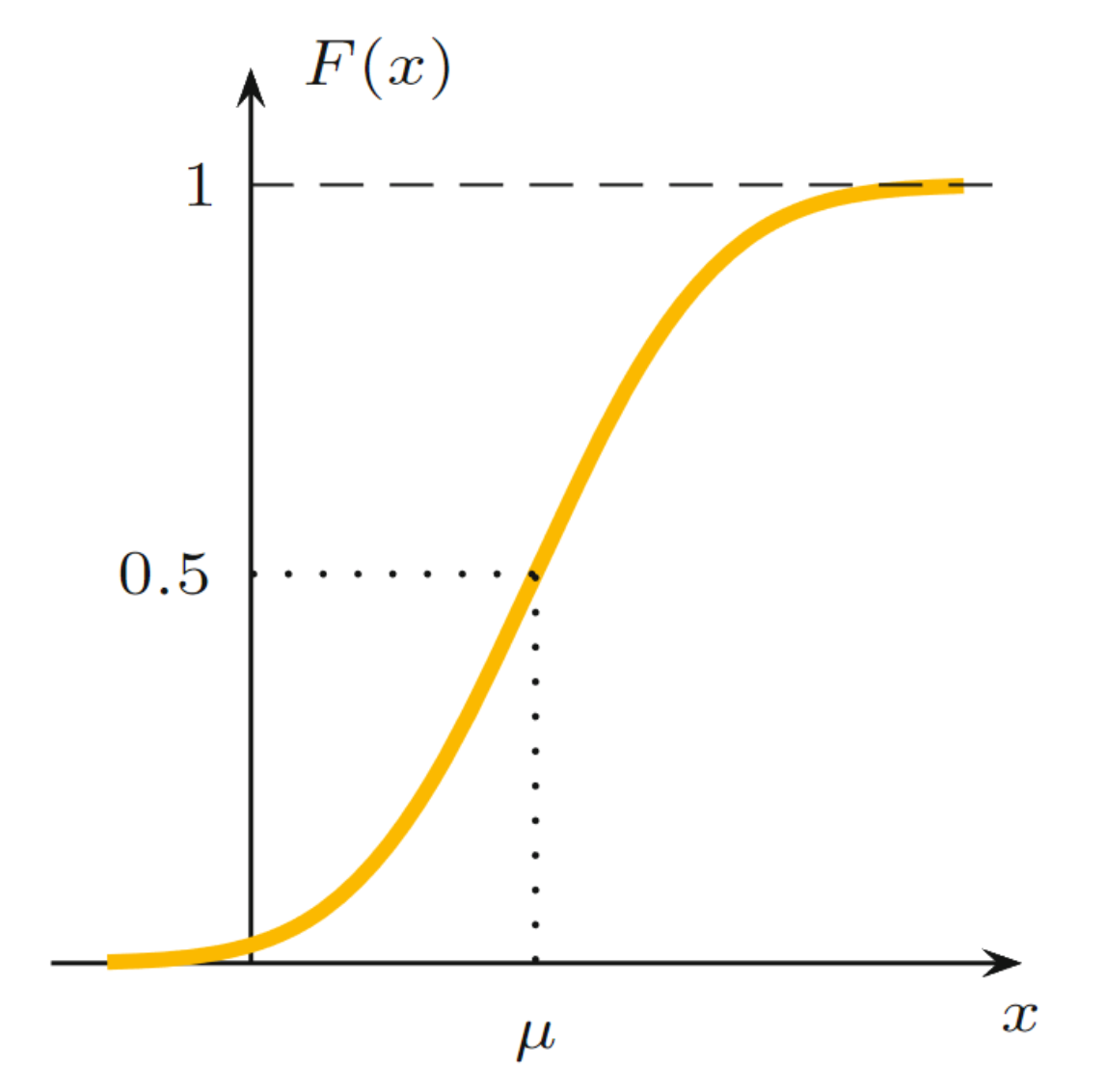
Folgende Abbildung zeigt die Verteilungsfunktion der Normalverteilung¹

Footnotes

1. @henze2019, p. 137 ↩ ↩²