Definition - Standardnormalverteilung

• Typen:
  • Normalverteilung
• Konstrukte:
  • z-Score
  • Konfidenzintervall im Produktmodell
  • Konfidenzintervall im Binomialmodell
  • Chi-Quadrat-Verteilung (siehe Chi-Quadrat-Verteilung als Summe Standardnormalverteilter Zufallsvariablen)
• Generalisierungen:
  • Normalverteilung
  • Dichte einer stetigen Zufallsvariable
  • Absolut stetige Verteilungsfunktion einer Zufallsvariablen
• Hinreichende Bedingungen:
  • Zentraler Grenzwertsatz
• Involvierte Definitionen:
  • Absolut stetige Verteilungsfunktion einer Zufallsvariablen
• Veranstaltung: @henze2019
• Referenz: EiS

⠀

Definition: Standardnormalverteilung

Wir bezeichnen die Zufallsvariable als standardnormalverteilt, wenn , wenn die folgende Dichte besitzt:

Definition: Verteilungsfunktion der Standardnormalverteilung

Sei eine standardnormalverteilte Zufallsvariable.
Sei die Dichte von .

Da der Ausdruck nicht elementar integrierbar ist, kann auch die Verteilungsfunktion der Standardnormalverteilung nicht direkt angegeben werden.

Daher setzen wir als Verteilungsfunktion von :

Leider lässt sich die Funktion nicht elementar integrieren, weshalb es für auch keine in geschlossener Form angebbare Stammfunktion gibt.

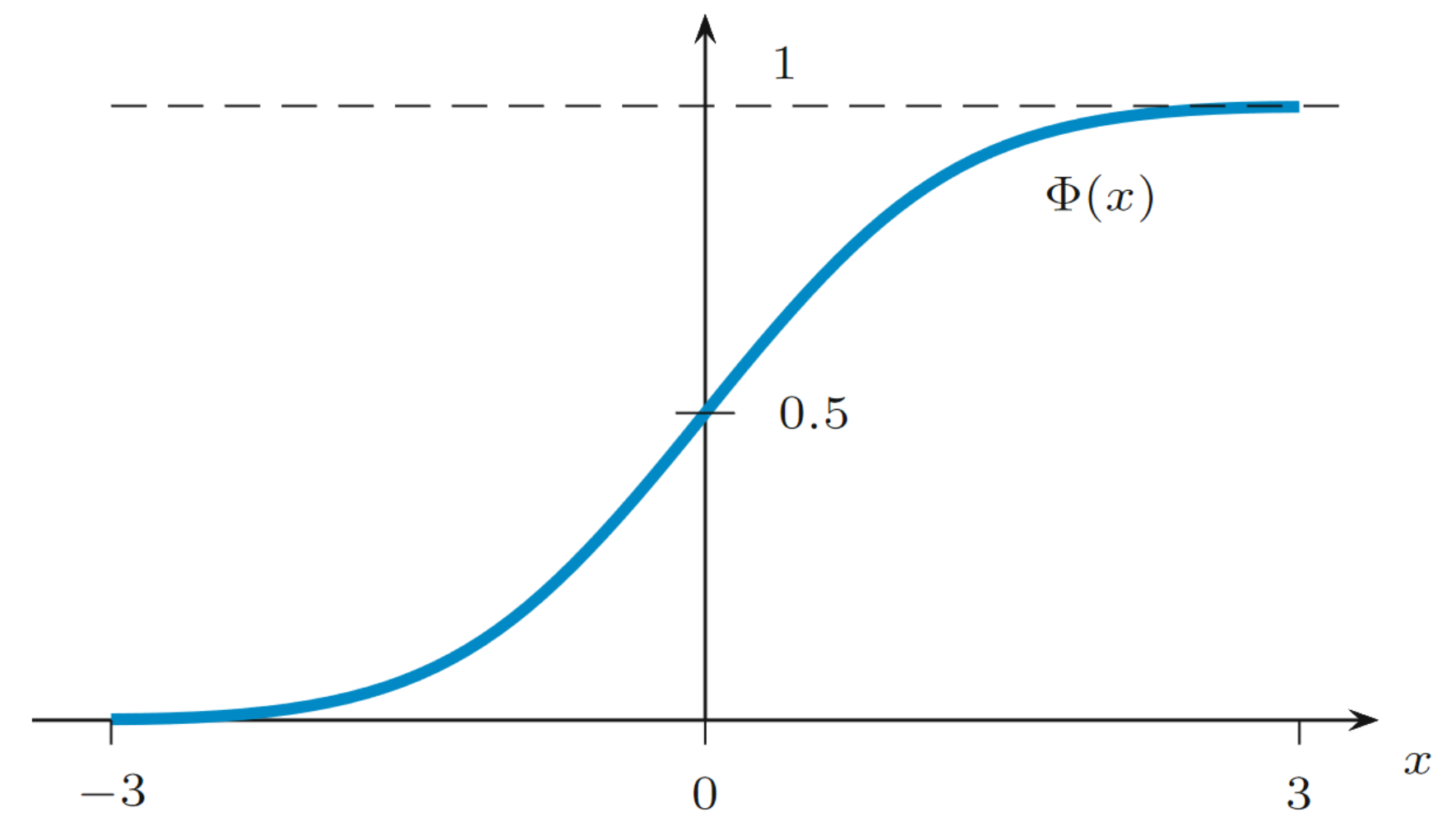
Zur Bestimmung von sind daher in der Regel Tabellen gegeben.

Folgende Abbildung zeigt die Verteilungsfunktion der Normalverteilung¹

Proposition: Symmetrie der -Funktion

Es gilt:

Anmerkung

Quantile der Standardnormalverteilung

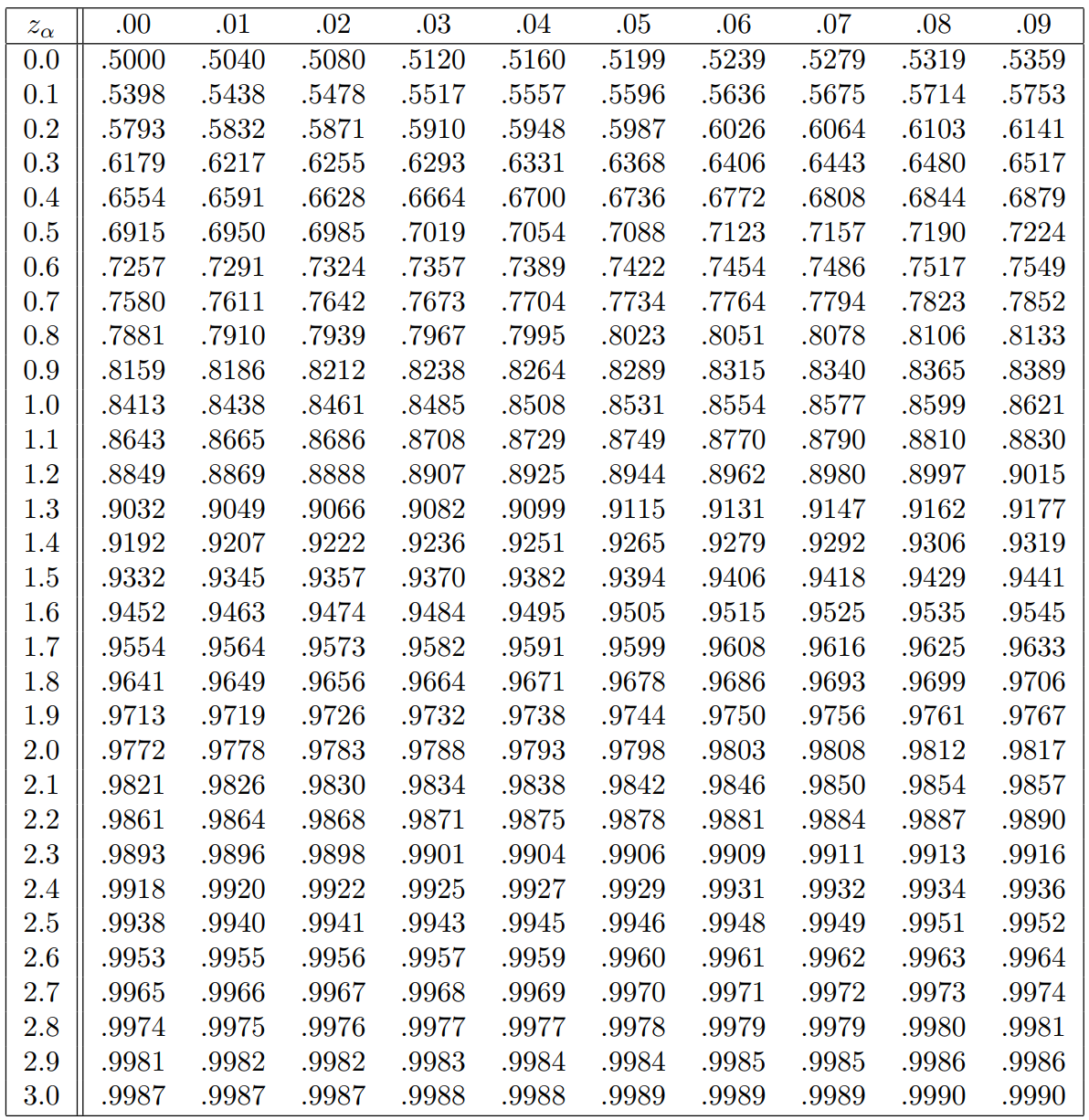
Ablesen von Werten aus der Verteilungstabelle

Angenommen, sei ein -Quantil der Standardnormalverteilung, also .

Dann erhalten wir den Wert von in dem wir:

1. den -Wert im Inneren der Tabelle suchen
2. Summe aus - und -Wert der Tabelle ergibt dann den Wert

und den Wert erhalten wir, in dem wir

1. den -Wert in eine Summe aus - und -Achse zerlegen

2. die Zelle in der Matrix Suchen, die zu dem - und -Wert passt.

• Ist gegeben als . Dann weißt uns die Kombination auf den Wert .
• Ist gegeben als , so finden wir als Summe von .

Ablesen von Werten, die gar nicht in der Verteilungstabelle stehen (Symmetrie)

Aufgrund der Symmetrie der Standardnormalverteilung gilt

• Ist gegeben als , so schauen wir erstmal in dem Eintrag mit und . Hier finden wir . Das richtige erhalten wir jetzt durch
• Ist geben als , so berechnen wir zunächst . So erhalten wir . Das richtige ist dann .

Quantile von der Uni Ulm

Die Uni-Ulm hat eine noch mal deutlich angenehmere Tabelle:

Footnotes

1. @henze2019, p. 137 ↩