Definition - Chi-Quadrat-Verteilung

• Konstrukte:
  • Linksseitiger Chi-Quadrat-Test auf die Varianz
  • Rechtsseitiger Chi-Quadrat-Test auf die Varianz
  • Linksseitiger Chi-Quadrat-Test auf die Varianz mit geschätztem Erwartungswert
  • Chi-Quadrat-Anpassungstest
  • Chi-Quadrat-Unabhängigkeitstest
• Generalisierungen:
  • Gamma-Verteilung
  • Exponentialfamilie
• Hinreichende Bedingungen:
  • Chi-Quadrat-Verteilung als Summe Standardnormalverteilter Zufallsvariablen
• Involvierte Definitionen:
• Veranstaltung: MatheDS
• Referenz:
  • @riedel2023 (Definition 6.2.23)
  • @henze2019 (p. 157)

⠀

Definition: Dichte der Chi-Quadrat-Verteilung

Wir bezeichnen die Zufallsvariable als Chi-Quadrat-verteilt mit Freiheitsgraden, kurz , wenn die folgende Dichte besitzt:

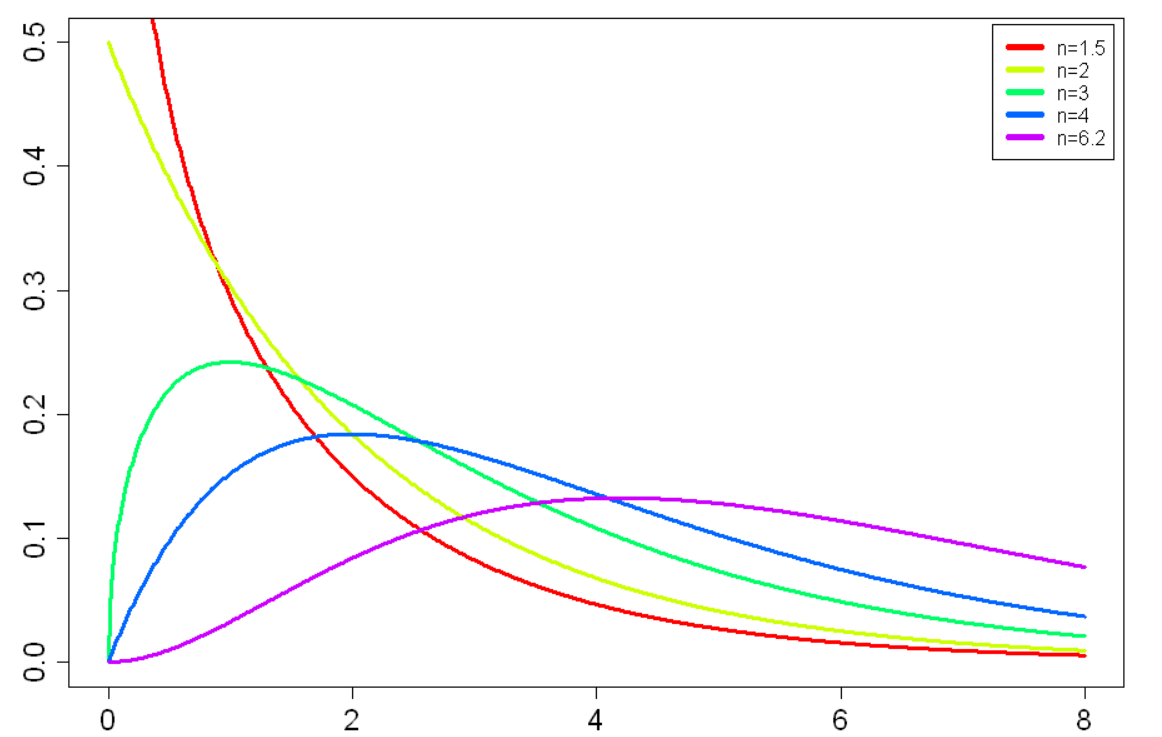
Die Chi-Quadrat-Verteilung ist ein Spezialfall der Gammaverteilung mit , also mit .

Die folgende Illustration zeigt die Dichte der Chi-Quadrat-Verteilung mit verschiedenen Freiheitsgraden¹:

Definition: Verteilungsfunktion der Chi-Quadrat-Verteilung

Als Spezialfall der Gammaverteilung gilt für die Verteilungsfunktion der Chi-Quadrat-Verteilung:

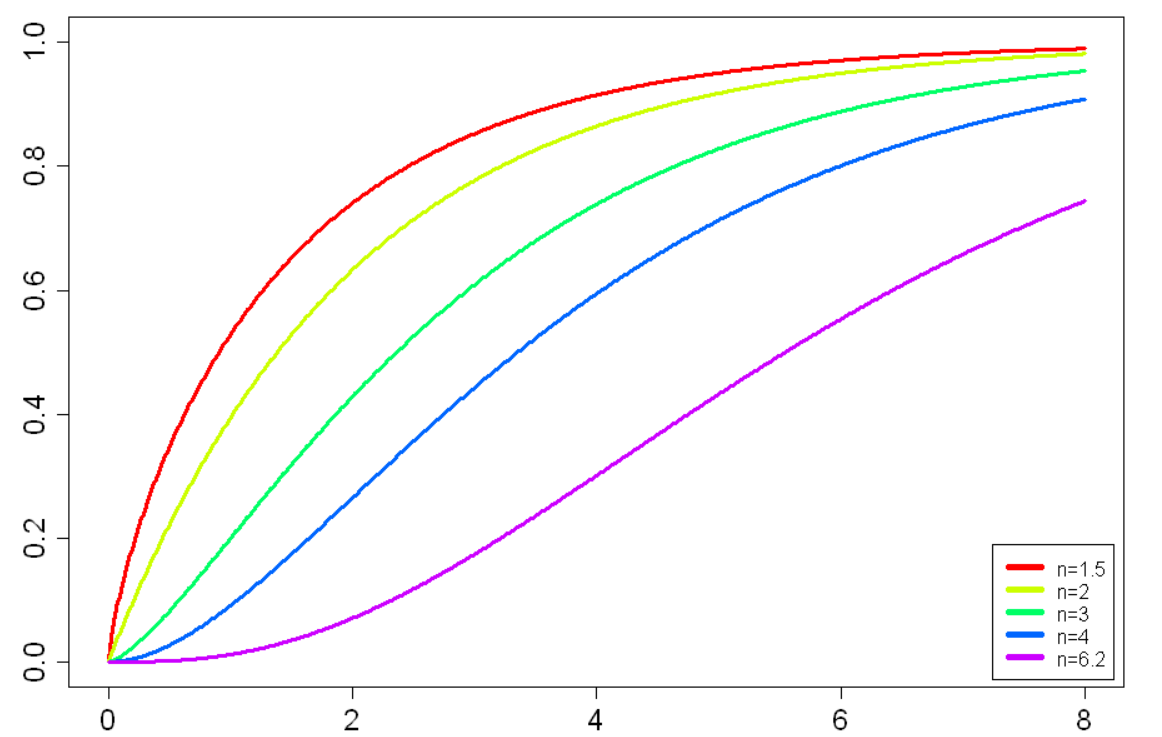
wobei die regularisierte unvollständige Gammafunktion ist, mit

Die folgende Illustration zeigt die Verteilungsfunktion der Chi-Quadrat-Verteilung mit verschiedenen Freiheitsgraden¹:

Anmerkung

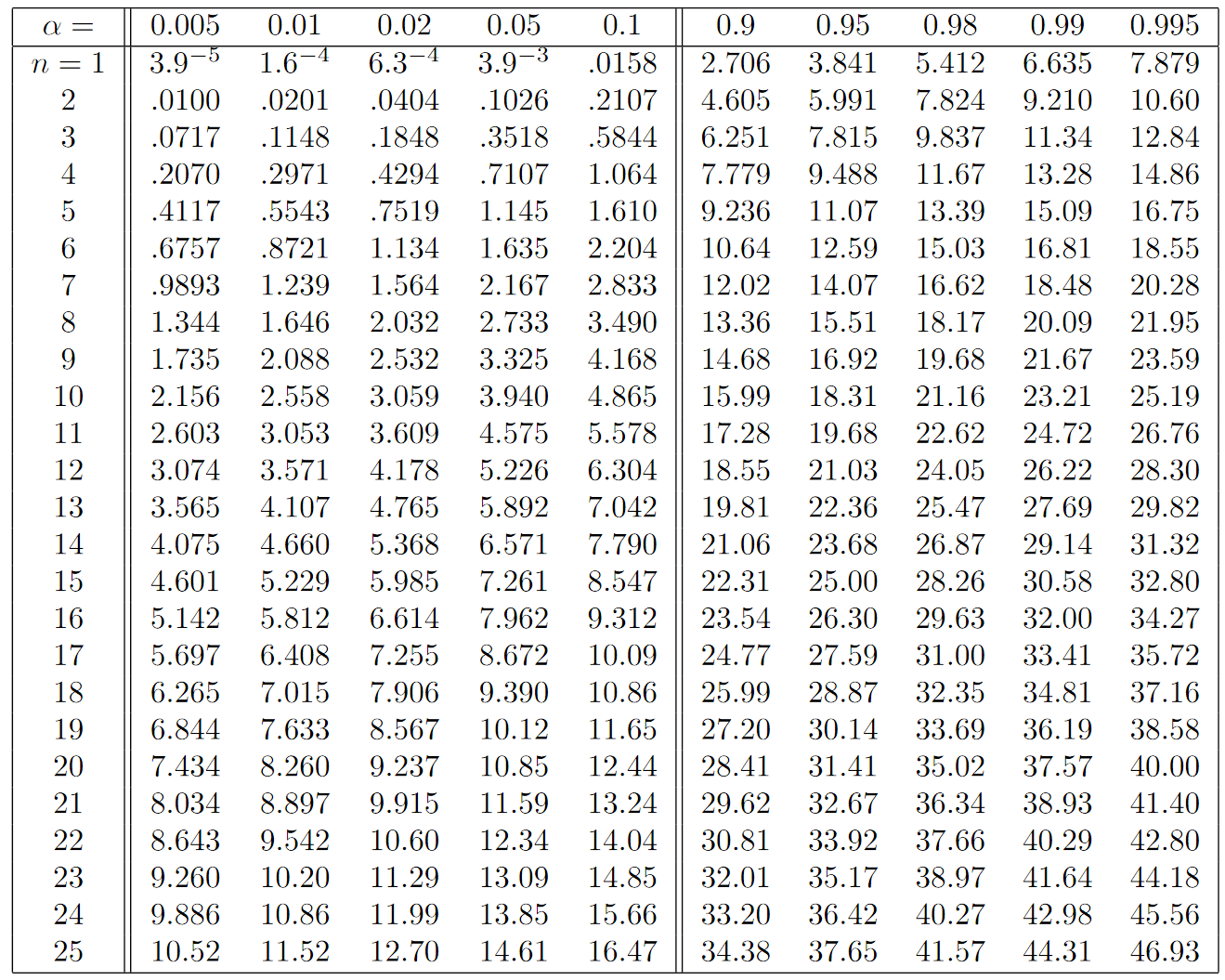
Quantile der Chi-Quadrat-Verteilung

Footnotes

1. Wikipedia “Thomas Steiner”, https://de.wikipedia.org/wiki/Datei:Chi-Squared-pdf_and_cdf.png ↩ ↩²