Definition - Injektivität

• Beispiele:
  • Exponentialfunktion
  • Logarithmus
• Eigenschaften:
  • Injektive stetige Funktionen über einem abgeschlossenen Intervall sind streng monoton
  • Injektive stetige Funktionen über einem beliebigen Intervall sind streng monoton
• Hinreichende Aussagen:
  • Streng monotone Funktionen sind injektiv
• Charakterisierungen:
  • Bemerkung - Funktion ist invertierbar gdw Funktion ist injektiv
  • Korollar - Stetige Funktion über einem Intervall ist injektiv gdw Stetige Funktion über einem Intervall ist streng monoton
• Involvierte Definitionen:
  • Abbildung
  • Bild
  • Urbild
• Referenz: } Mathematische Grundlagen KE1 - Abbildungen

⠀

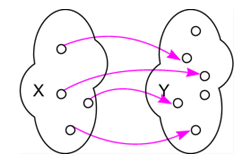
Definition: Injektivität

heißt injektiv, wenn jedes Element im Bild von höchstens ein Urbild hat.

Anmerkung

Injektivität beweisen

Um die Injektivität zu beweisen, muss man

1. Ein beliebiges Element wählen
2. Annehmen, dieses Element hätte die Urbilder und
3. Zeigen, dass .

Injektivität widerlegen

Um die Injektivität zu widerlegen, reicht es aus, zwei > verschiedene und zu finden für die gilt .