Merkregel - Graphen einer Umkehrfunktion ermitteln

• Involvierte Definitionen:
  • Umkehrfunktion
  • Graph
  • Injektivität
• Referenz: Mathegrundlagen

⠀

Merkregel: Wie man den Graph einer Umkehrfunktion ermitteln kann

Sei eine injektive Funktion.

Den Graph von erhalten wir, indem wir den Graph von an der Diagonalen spiegeln.

Beweis

Der Graph von ist die Menge . Der Graph von ist die Menge .

Das bedeutet, dass die Koordinaten der Punkte des Graphen vertauscht werden. Quasi: .

Geometrisch können wir diese Vertauschung anhand der folgenden Skizze aus dem Skript interpretieren.

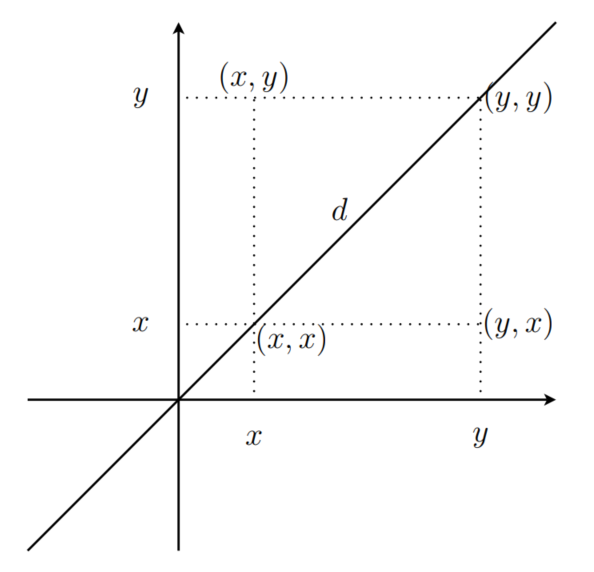
Die Vertauschung ist hier nichts anderes als die Spiegelung des Punktes an der Diagonalen - was zu zeigen war.