Definition - Matrizenmultiplikation

• Entspricht in der abstrakten linearen Algebra:
  • Komposition von Homomorphismen
    • Siehe Proposition 9.3.1
• Konstrukte:
  • Invertierbare Matrix
• Eigenschaften:
  • Assoziativgesetz der Matrizenmultiplikation,
  • Distributivgesetze der Matrizenmultiplikation
  • Das neutrale Element der Matrizenmultiplikation
  • Invertierbarkeit von n x n Matrizen
  • Matrizenmultiplikation ist (k)eine Verknüpfung
  • Komposition linearer Abbildungen als Matrizenmultiplikation
• Referenz: } Mathematische Grundlagen KE1 - Matrizenmultiplikation

Definition: Matrizenmultiplikation

Seien und zwei Matrizen mit

So ist die Multiplikation definiert durch

und

WARNING

Die Multiplikation ist immer dann gestattet, wenn gilt: und . Für das Ergebnis gilt .

In anderen Worten:

• die Spaltenanzahl von muss mit der Zeilenanzahl in übereinstimmen.
• Die Zeilenanzahl von stimmt mit und die Spaltenanzahl mit überein.

Berechnung

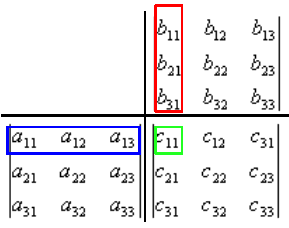
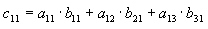
Visuell gilt: wir multiplizieren die Einträge aus Zeile von mit den Einträgen aus Spalte von und Summieren die Ergebnisse:

Als Algorithmus

Um zu berechnen:

1. -te Zeile von und
2. -te Spalte von transponieren ⇒
3. übereinander legen und ausmultiplizieren:

Anmerkung

Alternative Betrachtungen

Als Linearkombination von Spalten

Wir können die Multiplikation

auch als Linearkombination von Spalten betrachten: Etwas komplexer kann die Multiplikation

ebenfalls als Linearkombination von Spalten betrachtet werden:

Als Linearkombination von Zeilen

Genauso können wir die Matrixmultiplikation als Linearkombination von Zeilen betrachten:

als

Etwas komplexer kann die Multiplikation

ebenfalls als Linearkombination von Zeilen betrachtet werden:

Beispiele

Beispiel 1 Seien und . So gilt

und

Beispiel 2 Seien

So gilt . Da Gilt

Beispiel 3 Seien

So gilt . Da gilt