Definition - Studentsche t-Verteilung

• Typen:
  • Standard-Cauchy-Verteilung für
• Konstrukte:
  • Studentisierung
  • Linksseitiger t-Test auf den Erwartungswert
  • Rechtsseitiger t-Test auf den Erwartungswert
  • Beidseitiger t-Test auf den Erwartungswert
  • Konfidenzintervall im Gaußschen Produktmodell
• Generalisierungen:
  • Absolut stetige Verteilungsfunktion einer Zufallsvariablen
  • Dichte einer stetigen Zufallsvariable
  • Stetige Zufallsvariable
• Involvierte Definitionen:
  • Eulersche Beta-Funktion
  • Absolut stetige Verteilungsfunktion einer Zufallsvariablen
  • Dichtefunktion
• Veranstaltung: MatheDS
• Referenz: @riedel2023

⠀

Definition: Dichte der Studentsche -Verteilung mit Freiheitsgraden

Wir bezeichnen die Zufallsvariable als Student -verteilt mit -Freiheitsgraden, kurz , wenn die folgende Dichte besitzt:

Anmerkung

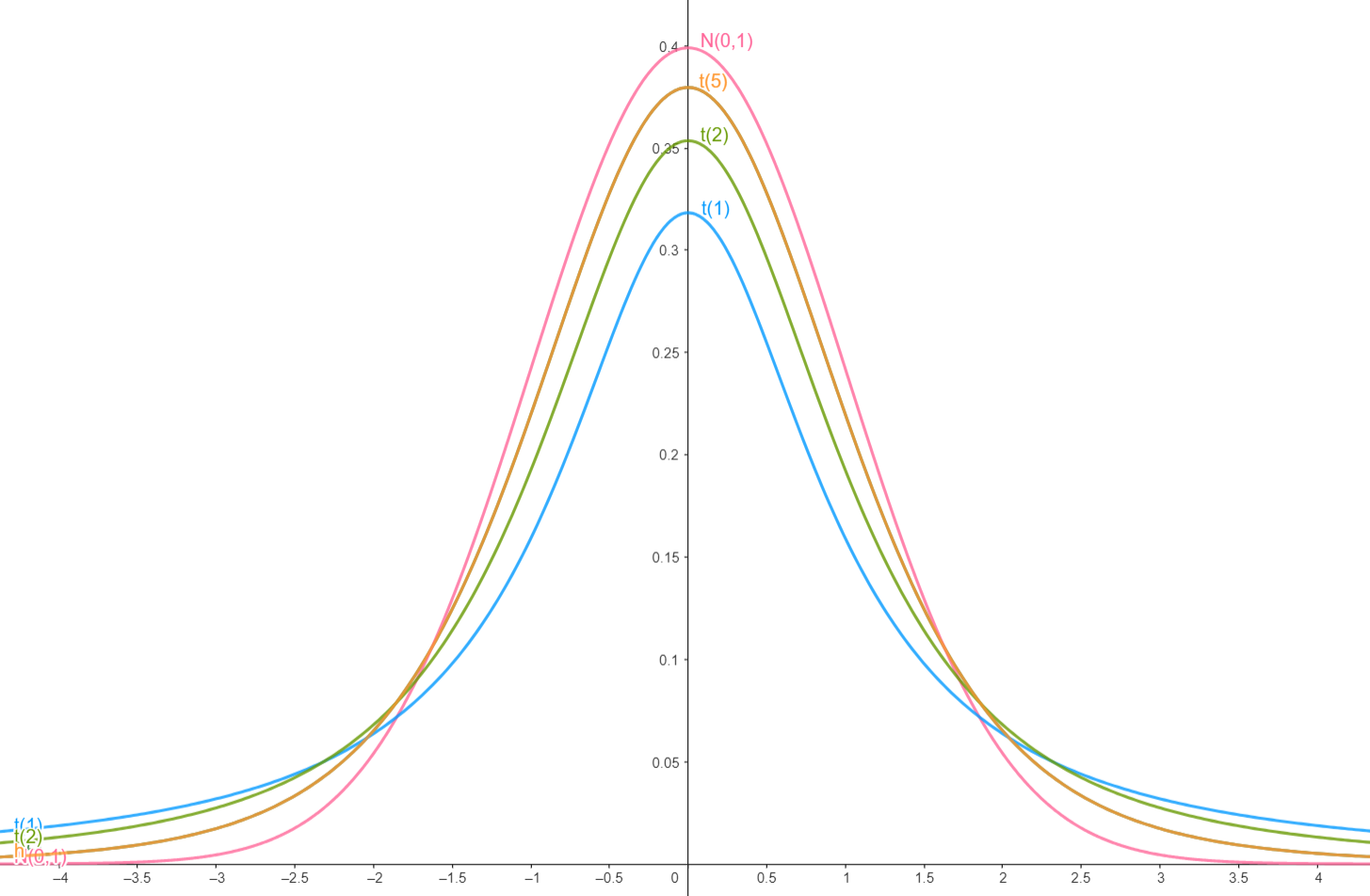
Illustration: Dichte der studentschen -Verteilung vs. Dichte der Standardnormalverteilung

Die folgende Abbildung plottet die Dichte der -Verteilung für die Freiheitsgrade gegen die Dichte der Standardnormalverteilung :

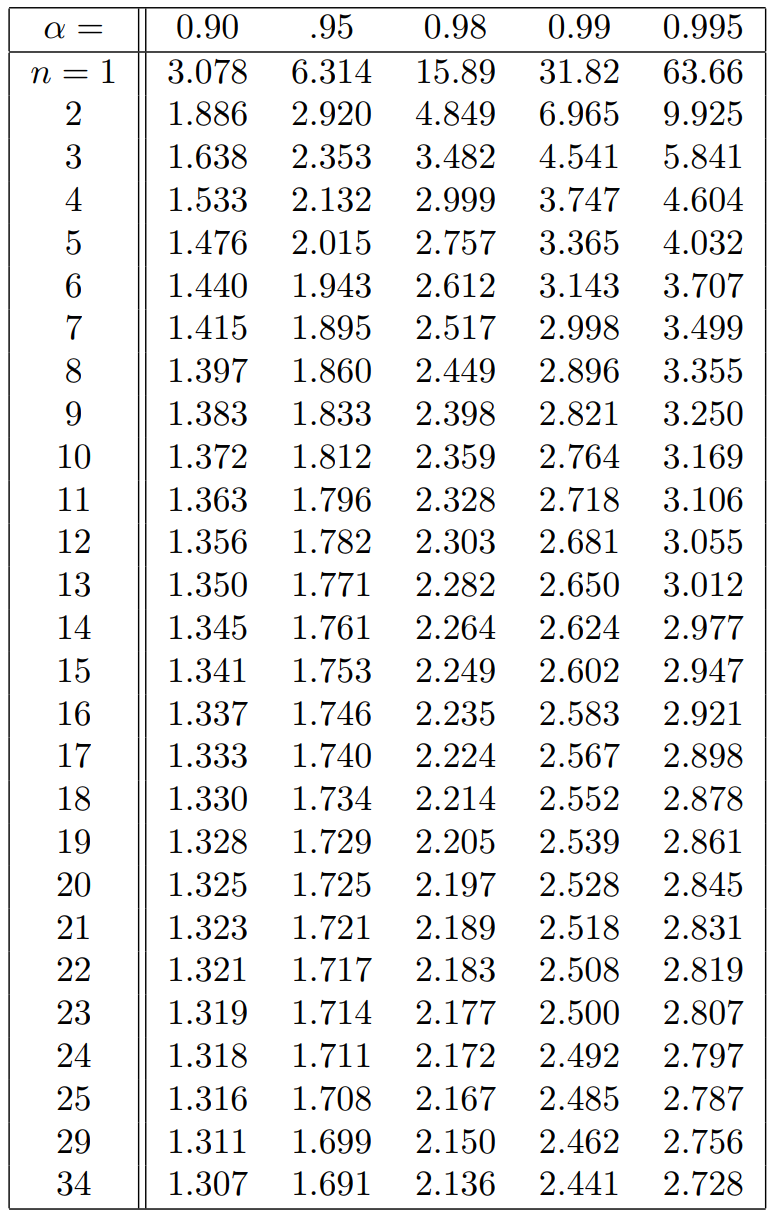
Quantile der studentschen -Verteilung

Beispiele für die Bestimmung von Quantilen

Sei ein -Quantil der studentschen -Verteilung mit -Freiheitsgraden.

Einfache Bestimmung

Bestimme für . Es gilt:

Bestimmung unter Ausnutzung der Symmetrie

Bestimme für .

Wir bestimmen zunächst für : Aufgrund der Symmetrie der studentschen -Verteilung gilt: