Bewiesen durch:Generalisierungen:Referenz: } Mathematische Grundlagen KE2 - Der Rang einer Matrix
Proposition 4.5.5: Abschätzung von Rängen
Sei
, Dann gilt:
- Wenn
invertierbar ist, so gilt - Wenn
invertierbar ist, so gilt - Wenn
mit und , so gilt
Beweis
Wenn
Sei
Sei
Das heißt auch, dass
Sei
Dann gilt nach dem Satz 4.4.2, dass
Wenn
Sei
und für
Das heißt:
Wenn wir zusammenführen und substituieren:
Diese Ungleichungskette kann nur gelten, wenn alle Abschätzungen
Es gilt also:
Wenn
Sei
Es gilt
Daraus folgt, dass das Produkt
Das folgt direkt aus der Definition der Matrizenmultiplikation, Visualisierung bspw. nach Falk-Schema:
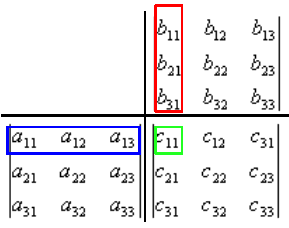
Es gilt also: