Definition - Matrixdarstellung der zweidimensionalen diskreten Faltung

• Typen:
  • Valides Padding
  • Halbes Padding
  • Vollständiges Padding
  • Stride
  • Depthwise Convolution
• Konstrukte:
  • Kernelmatrix
  • Feature Map
  • Convolutional Neural Network
  • Conv-Layer
• Generalisierungen:
  • Zweidimensionale diskrete Faltung
• Involvierte Definitionen:
  • Frobenius-Skalarprodukt
  • Untermatrix
  • Translationsinvarianz
• Veranstaltung: EML
• Referenz: @thimm2024 (Abschnitt 5.2.1)

⠀

Definition: Matrixfaltung

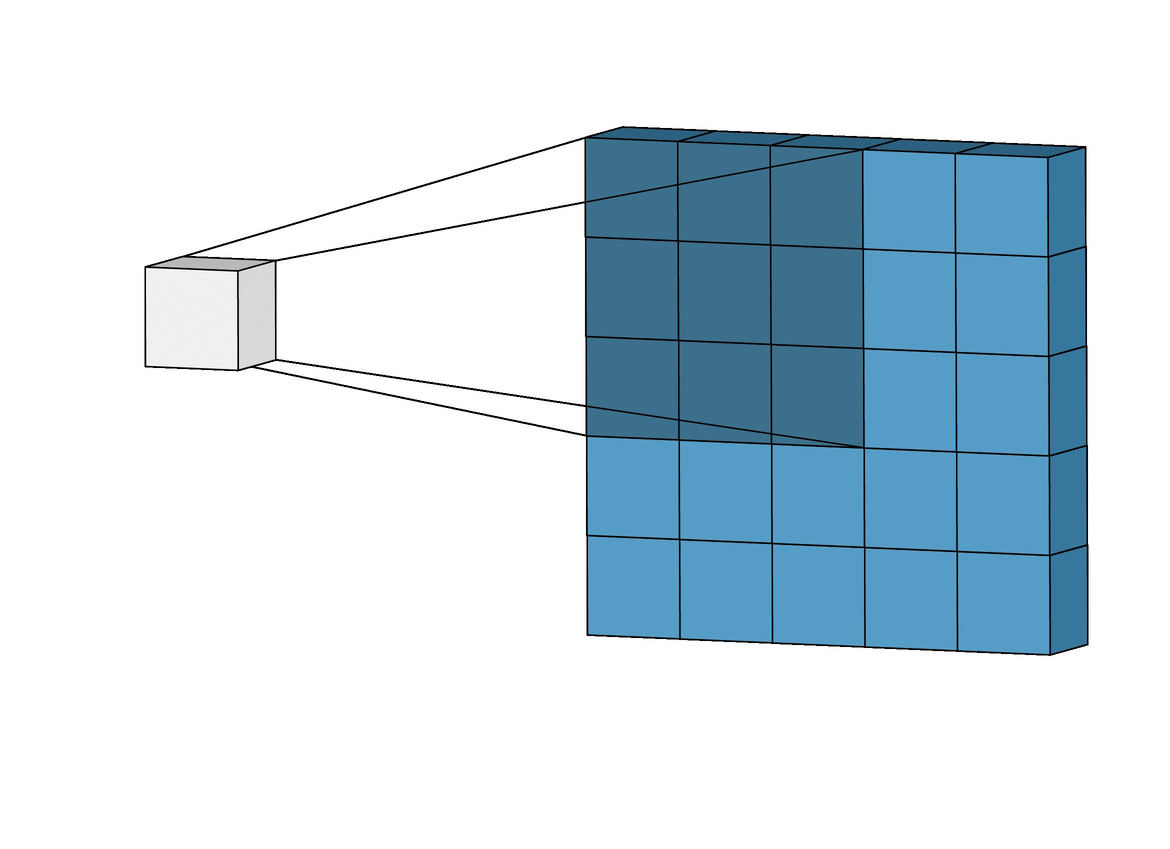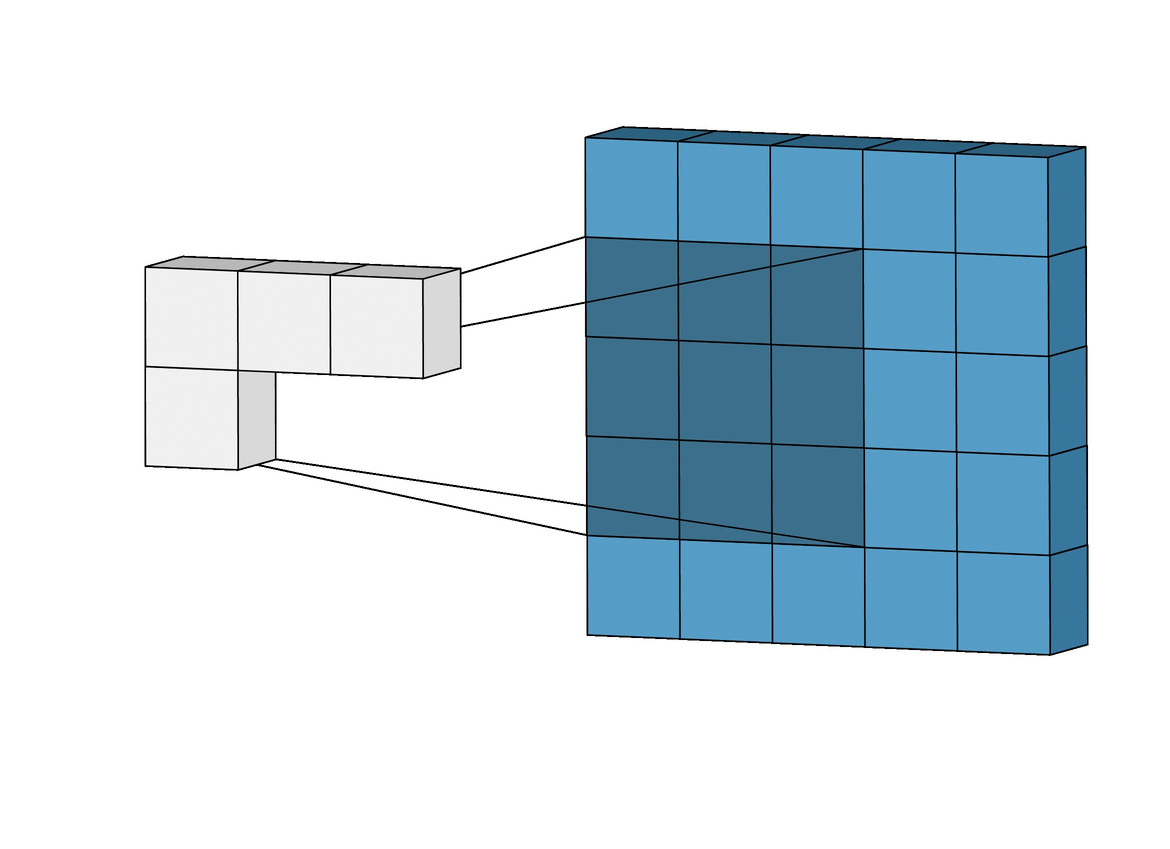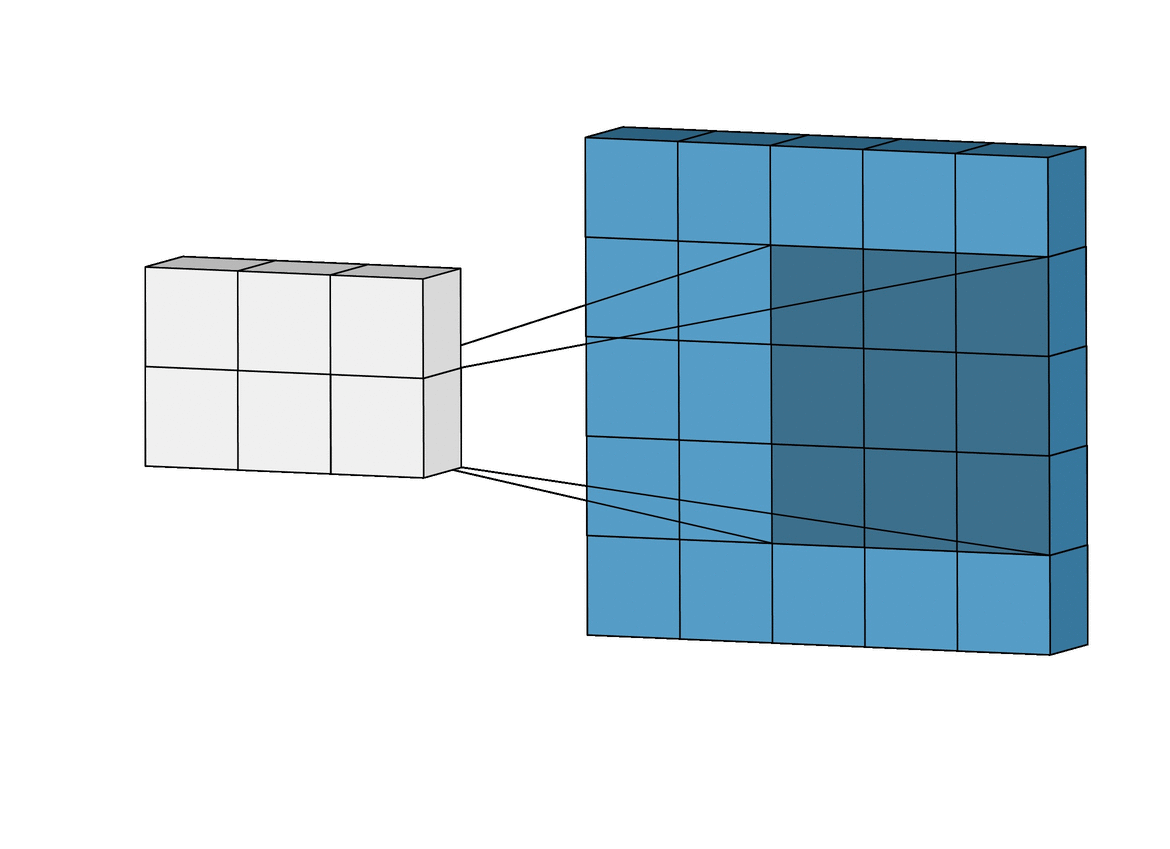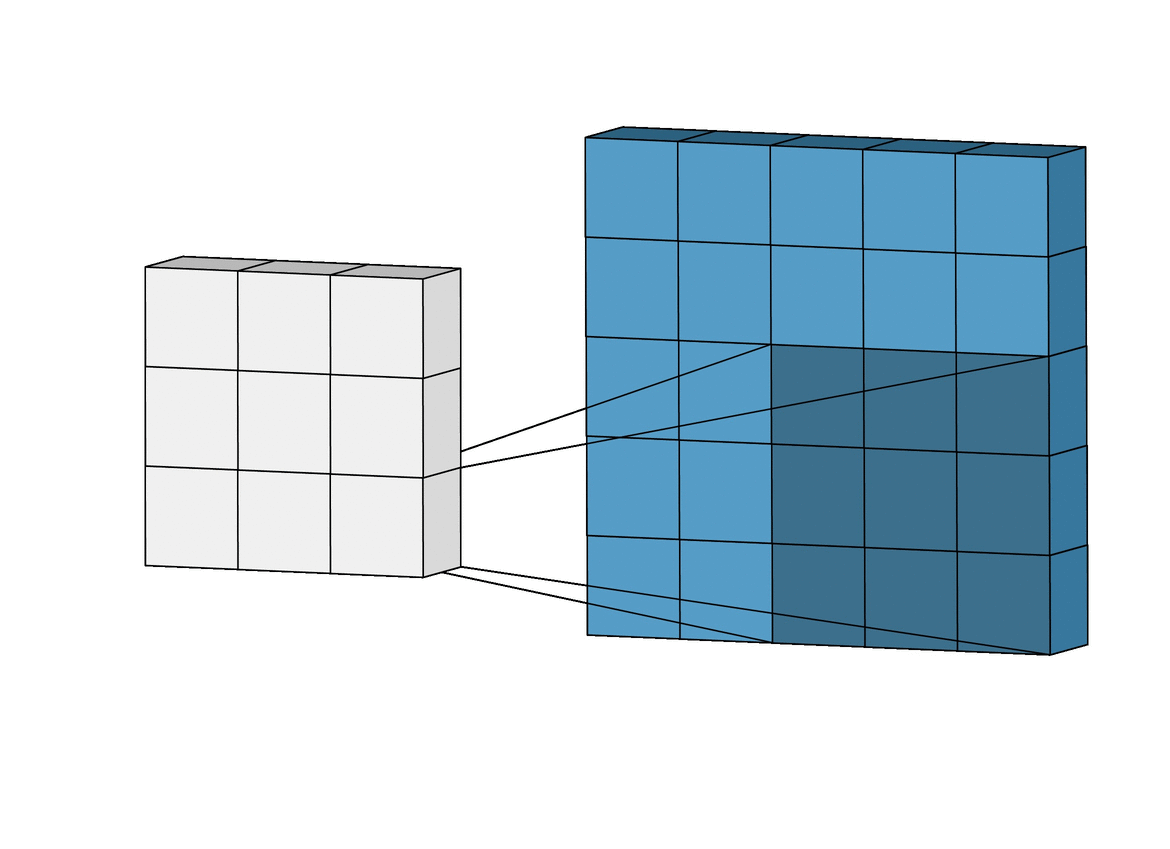
Da die Faltungsoperation in der Regel lokal ist¹, lässt sie sich als Matrixoperation darstellen. Wir sprechen an dieser Stelle auch von Matrixfaltung oder Matrix-Convolution.

Sei die Eingabefunktion.
Sei die Matrixdarstellung der Eingabefunktion.

Sei die Filterfunktion.
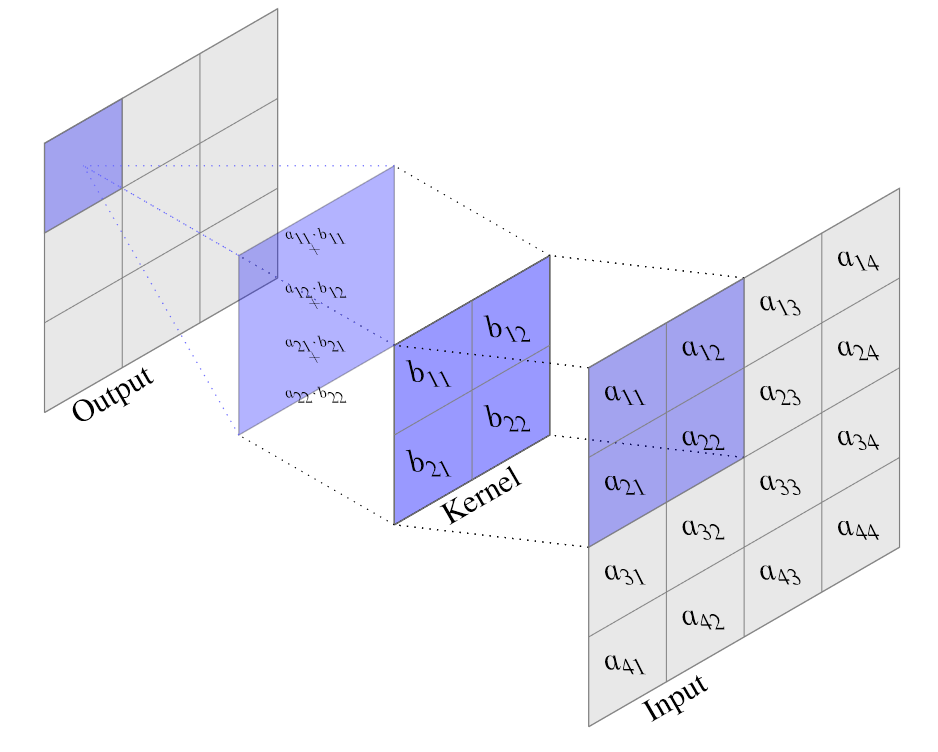
Sei die Matrixdarstellung der Filterfunktion.

Zur Berechnung der gefalteten Matrix wird die Filtermatrix Schrittweise (en. Stride) über die Inputmatrix geschoben.

In jedem Schritt wird das Frobenius-Skalarprodukt zwischen dem “überdeckten” Teil der Matrix und dem Filter berechnet.

Die Ergebnisse des Skalarproduktes bilden anschließend die Einträge von .

Im einfachsten Fall beträgt die Schrittweite und der Filter bedeckt stets vollständig (kein Padding):

Für den Eintrag der gefalteten Matrix erhalten wir also:

Anmerkung

Faltung und Untermatrix

Die Faltung kann als Frobenius-Skalarprodukt aller -dimensionalen Untermatrizen von mit interpretiert werden.

Beispiel: Glättungsfilter

Eine klassische Anwendung der zweidimensionalen diskreten Faltungsoperation sind Glättungsfilter.

Ein Beispiel für einen solchen Glättungsfilter ist der Kernel

Die Matrixdarstellung erhalten wir durch

Sei eine Eingabematrix gegeben durch

Dann erhalten wir die Feature Map durch

Die Berechnung erfolgt durch das Schema

Footnotes

1. Lokalität bedeutet in diesem Kontext, dass die zur Berechnung verwendete Umgebung auf wenige umgebende Werte beschränkt ist. ↩