Definition - Conv-Layer

• Typen:
  • 1x1-Conv-Layer
  • Depthwise Convolution
• Konstrukte:
  • Convolutional Neural Network
  • Feature Map
  • Receptive Field
• Generalisierungen:
  • Layer
• Eigenschaften:
  • Darstellung eines Conv-Layers als neuronales Netzwerk
• Involvierte Definitionen:
  • Matrixfaltung
  • Aktivierungsfunktion
  • ReLU-Aktivierungsfunktion
  • Translationsinvarianz
  • oft gefolgt von einer Pooling-Operation
• Veranstaltung: EML
• Referenz: @thimm2024 (Abschnitt 5.2.3, 5.2.4)

⠀

Definition: Conv-Layer

Als Conv-Layer (auch Faltungsschicht) bezeichnen wir eine Schicht in neuronalen Netzwerken, die auf den Eingabedaten eine Matrixfaltung ausführt.

Dabei werden Filter (Kernels) über die Eingabe verschoben, um Merkmale wie Kanten, Texturen und Muster zu extrahieren. Auf jeden Wert der so erzeugten Feature Map wird anschließend noch eine Aktivierungsfunktion (i.d.R. ReLU) angewendet.

Charakteristische für Conv-Layer ist:

• Paramater-Sharing: Dadurch, dass ein Filter auf eine Vielzahl von Einträgen angewendet wird, werden die Gewichte zwischen den Neuronen geteilt.
• Lokalität/Sparse Interaction: In die Berechnung jedes Output-Wertes fließen nur wenige, nah beieinanderliegende Input-Werte ein.
• Translationsinvarianz: Da der Kernel gleichmäßig über das Bild geschoben wird, führt ein “Objekt” (Bildabschnitt/“Patch”) in der oberen linken Ecke zu dem gleichen Ergebnis wie ein identisches Objekt in der unteren rechten Ecke. Die Berechnung ist überall gleich.

Anmerkung

Conv-Layer auf RGB-Bilddaten?

Häufig werden Conv-Layer auf Bilddaten angewendet, die neben einer Höhe und Breite zusätzlich noch verschieden Farb-Channels (i.d.R. RGB) enthalten. Sei die Anzahl der Channels.

Diese Problematik wird in der Praxis meistens so behandelt, dass jeder Filter nicht nur zwei sondern drei dimensional ist, also .

In jedem Schritt (Stride) dieser 3-dimensionalen Matrix-Faltung gehen wir wie folgt vor:

1. Wir berechnen die Faltung der Filter mit der jeweiligen Untermatrix.
2. Wir summieren die Faltungsergebnisse über die Channels.
3. Wir addieren den Bias hinzu.

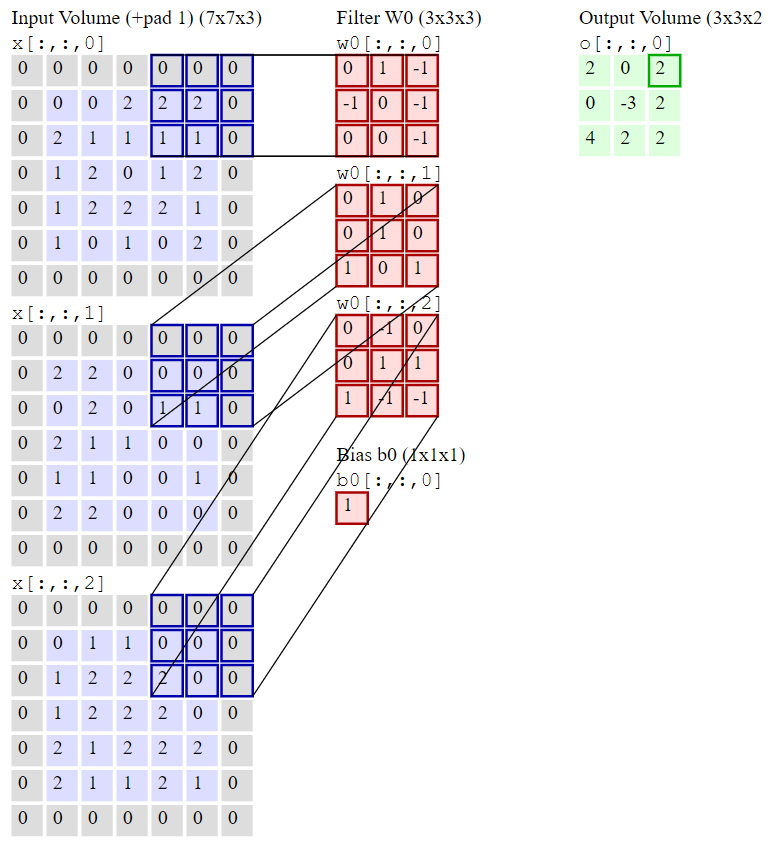
Machen wir es an dem folgenden Beispiel¹ ganz konkret:

In dem aktuellen Schritt gehen wir also wie folgt vor:

1. Faltungen: - die sind hier ziemlich einfach, weil die Einträge fast nur Nullen enthalten.

2. Summe über die Faltungen:

3. Bias hinzuaddieren:

4. Ergebnis:

Footnotes

1. https://cs231n.github.io/convolutional-networks/#conv ↩