Beispiele:Konstrukte:Involvierte Definitionen:- Modell (ML)
- Polynomielle Erweiterung
- Polynomielles Modell
- Bestimmtheitsmaß
- siehe auch Unteranpassung
- siehe auch Varianzfehler
Veranstaltung: EMLReferenz: @thimm2024 (Abschnitt 2.1.4, Lineare Regression - Über- und Unteranpassung)
⠀
Definition: Überanpassung im maschinellen Lernen
Im Allgemeinen bezeichnen wir ein Modell
als überangepasst, wenn es ein Modell gibt, so dass gilt:
hat einen kleineren Fehler auf den Testdaten hat einen kleineren Fehler auf allen anderen Daten
Definition: Überanpassung in der Statistik
In der Statistik bezeichnen wir ein Modell
als überangepasst, wenn es aufgrund seiner Komplexität so stark an die Trainingsdaten angepasst ist, dass es nicht mehr auf ungesehene Daten generalisieren kann. Überanpassung hat in diesem Sinne nichts mit der Anzahl der Trainingsdaten und der Länge des Trainings zu tun.
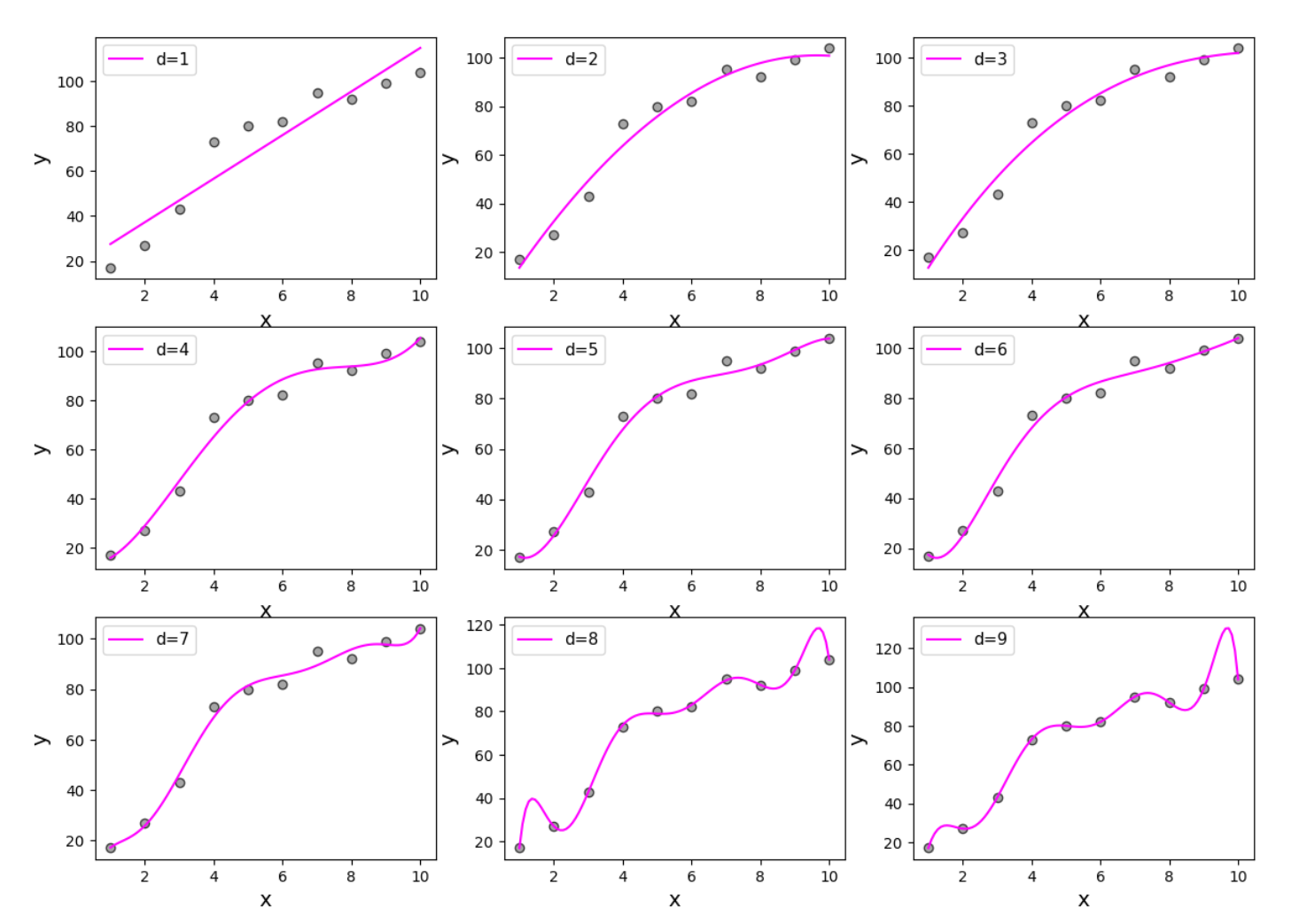
Hier am Beispiel eines polynomiellen Modells, wobei
der Maximalgrad der polynomiellen Erweiterung ist:
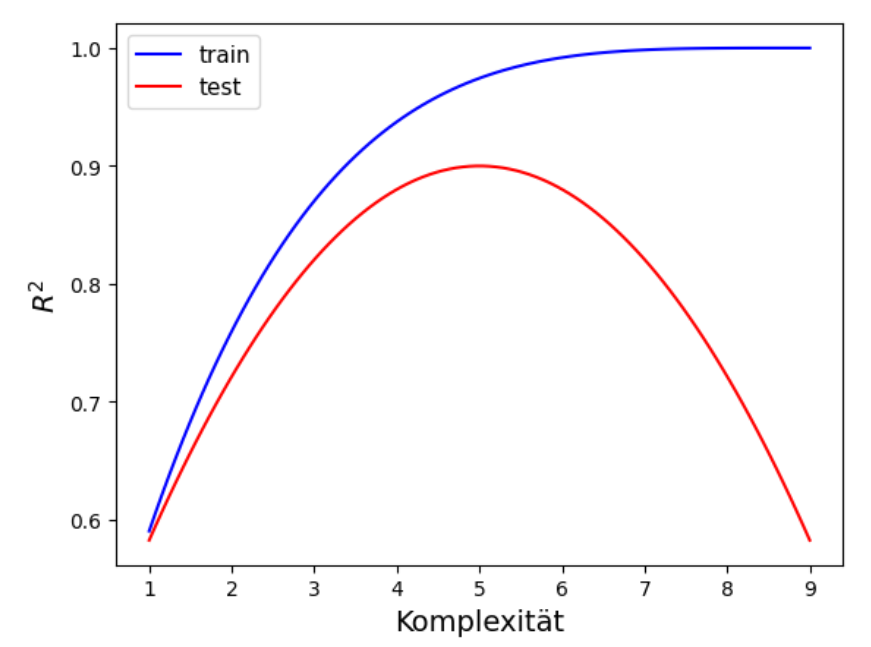
Idealtypisch gilt der folgende Zusammenhang, wobei
das Bestimmtheitsmaß sei und Komplexität die Anzahl der Parameter beschreibe:
Anmerkung
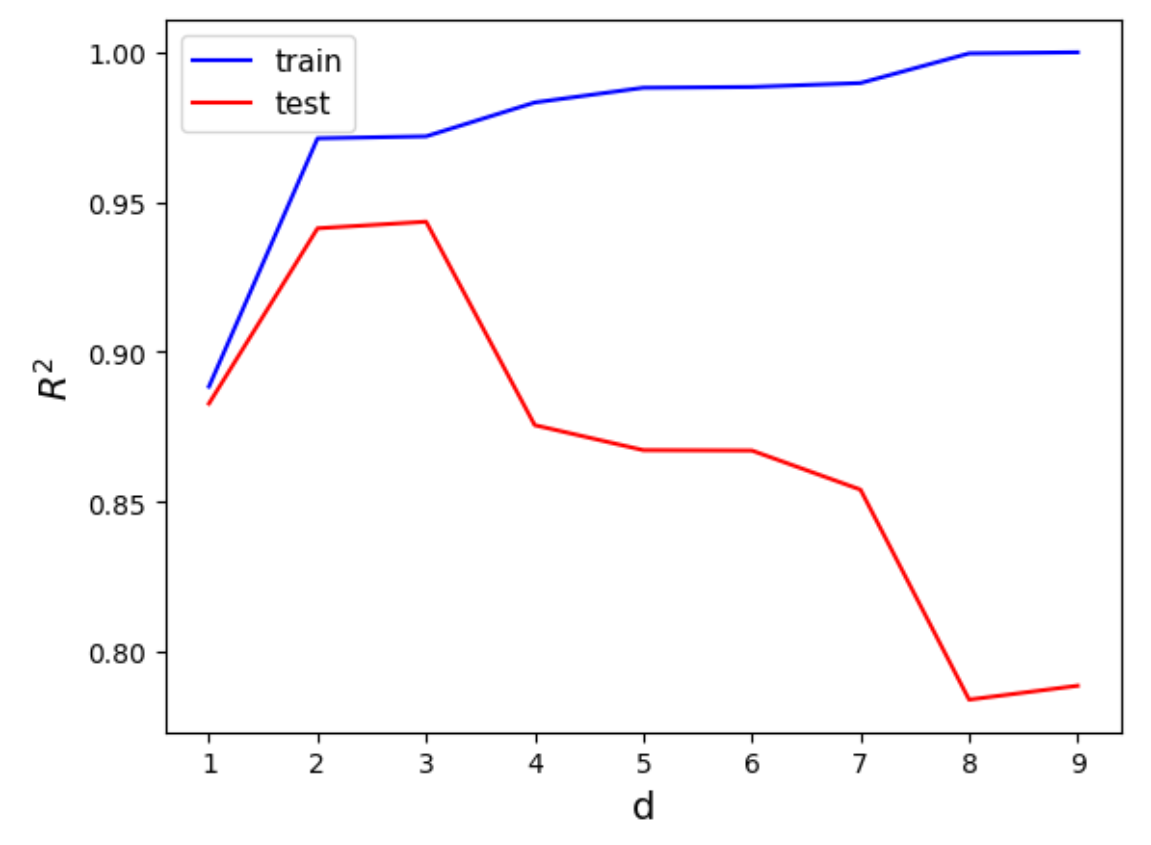
Konkretes Beispiel für den Zusammenhang zwischen Parameterzahl
Die Illustration über den Zusammenhang zwischen Parameterzahl (Komplexität) und Fehlerfunktion (hier
) war idealisiert. In einer konkreten Anwendung ergab sich beispielsweise der folgende Zusammenhang bei einer polynomiellen Regression: