Eigenschaften:Involvierte Definitionen:Referenz: } Mathematische Grundlagen KE1 - Abbildungen
⠀
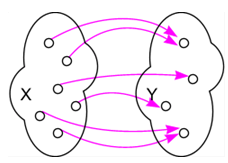
Definition: Surjektivität
heißt surjektiv (frz. sur “auf”), wenn jedes Element der Zielmenge im Bild von liegt. Oder in anderen Worten: jedes Element
hat ein Urbild unter .
Anmerkung
Beweisen von Surjektivität
Um Surjektivität zu beweisen, muss man
- mit einem beliebigen Element der Zielmenge,
beginnen ( ) - Ein Element
explizit angeben, für das gilt ( )
Widerlegen von Surjektivität
Um Surjektivität zu widerlegen, reicht es aus, ein einziges Element
anzugeben, das nicht im Bild von liegt.