/vault

Theorem - Berechnung der partiellen Ableitung bezüglich eines Gewichts

Aug 18, 202414 min read

⠀

Theorem: Berechnung der partiellen Ableitung bezüglich eines Gewichts

Sei ein gelabelter Datensatz.
Sei ein Neuronales Netzwerk gegeben mit

  • Schichten,
  • jeweils Neuronen pro Schicht und
  • Gewichten , wobei .

Sei der Fehler zwischen dem Label und der Vorhersage für ein Beispiel .

Wir erhalten die partielle Ableitung von bezüglich des Gewichtes zwischen

  • dem -ten Neuron der -ten Schicht und
  • dem -ten Neuron der -ten Schicht,
  • also

für ein Beispiel durch

Beweis

Abweichende Schreibweise

Im Folgenden benutzen wir Grant Sandersons Schreibweise

Wir führen den Beweis in zwei Teilen. Zunächst für ein vereinfachtes neuronales Netzwerk mit jeweils einem Neuron pro Layer. Dann für den generellen Fall.

Simples Netzwerk

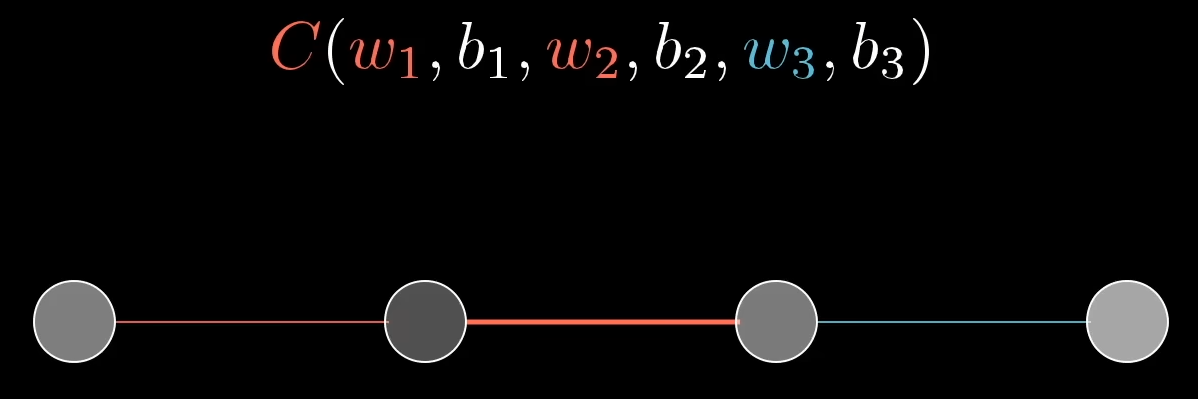
Sei ein simples Netzwerk mit drei versteckten Schichten gegeben. Jede Schicht enthalte genau ein Neuron. Als Fehlerfunktion wählen wir den quadratischen Fehler.

Konzentrieren wir uns zunächst nur auf die letzten beiden Neuronen:

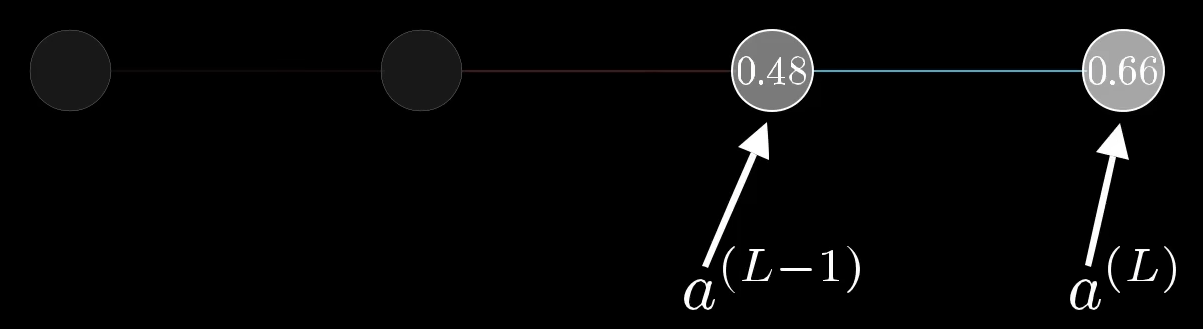
Die Werte und berechnen sich durch

wobei

Den Wert der Fehlerfunktion erhalten wir schließlich durch

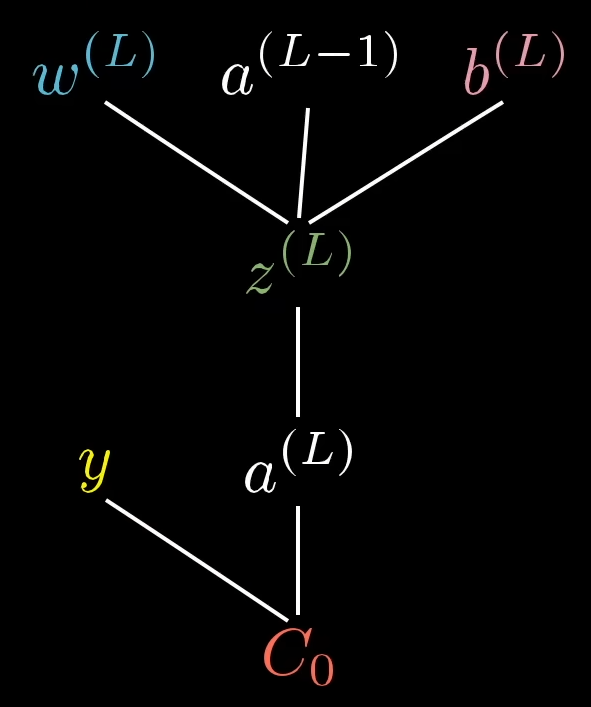
Für die Berechnung der Fehlerfunktion ließen sich die Inputs also wie folgt visualisieren:

Ableitung bezüglich des letzten Layers für

Wollen wir nun das Gewicht optimieren (bspw. mittels Gradient Descent), müssen wir die Partielle Ableitung von bezüglich , also bilden.

Mit Hilfe der Kettenregel erhalten wir diese durch

Das entspricht auch genau der Reihenfolge der Inputs:

  • ist Input für ,
  • ist Input für ,
  • ist Input für .

Wir berechnen nun nacheinander die jeweiligen partiellen Ableitungen:

Die komplette Ableitung erhalten wir also durch

Ableitung bezüglich des letzten Layers für

Wollen wir nun bezüglich ableiten, ersetzen wir einfach nur durch .

Für gilt:

Wir erhalten also:

Iteration für , ,

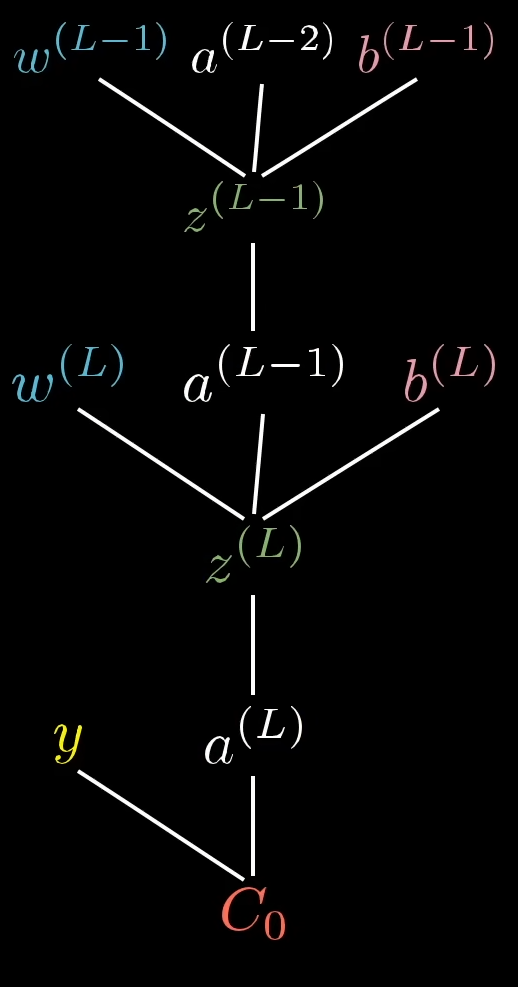
Wenn wir nun die Ableitung bezüglich benötigen, führen wir die Idee einfach fort. berechnet sich durch . Wieder als Diagramm aufgezeichnet:

Die Partielle Ableitung erhalten wir also durch

Allgemein gilt:

Generelles Netzwerk

Sei nun ein Neuronales Netzwerk mit mehreren Neuronen gegeben:

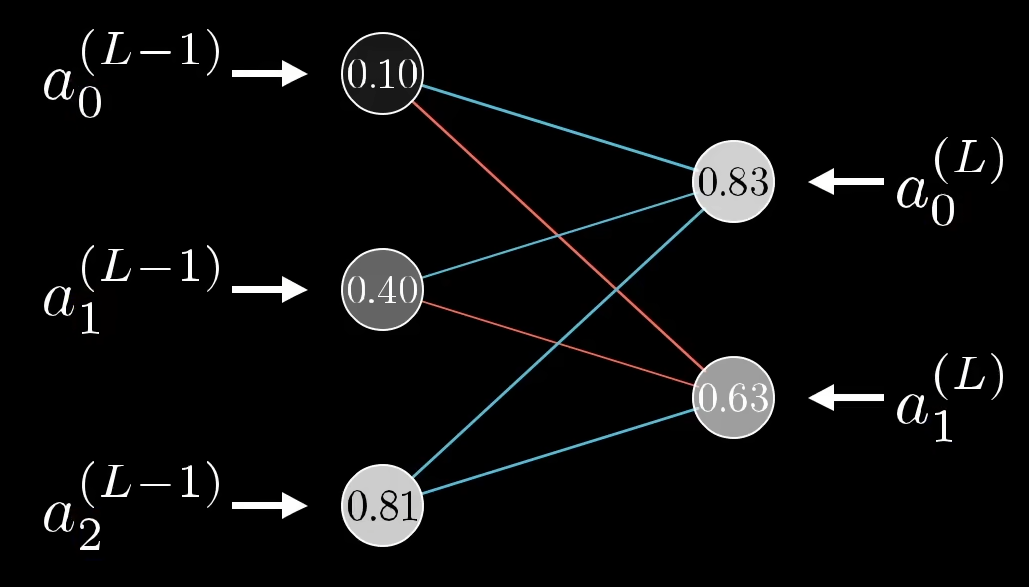
Die Werte und berechnen sich nun allgemein durch

wobei

Die Fehlerfunktion erhalten wir durch durch

Ableitung bezüglich des letzten Layers für

Wollen wir nun das Gewicht optimieren (bspw. mittels Gradient Descent), müssen wir die Partielle Ableitung von bezüglich , also , bilden.

Wie zuvor erhalten wir diese mit Hilfe der Kettenregel durch

Wir berechnen nun nacheinander die jeweiligen partiellen Ableitungen:

Interessanterweise sind die erhaltenen Ableitungen also annährend identisch zu dem Fall des einfachen Neuronalen Netzwerkes.

Die komplette Ableitung erhalten wir durch:

Die Ableitung bezüglich erhalten wir so wie etwas weiter oben.

Iteration für , ,

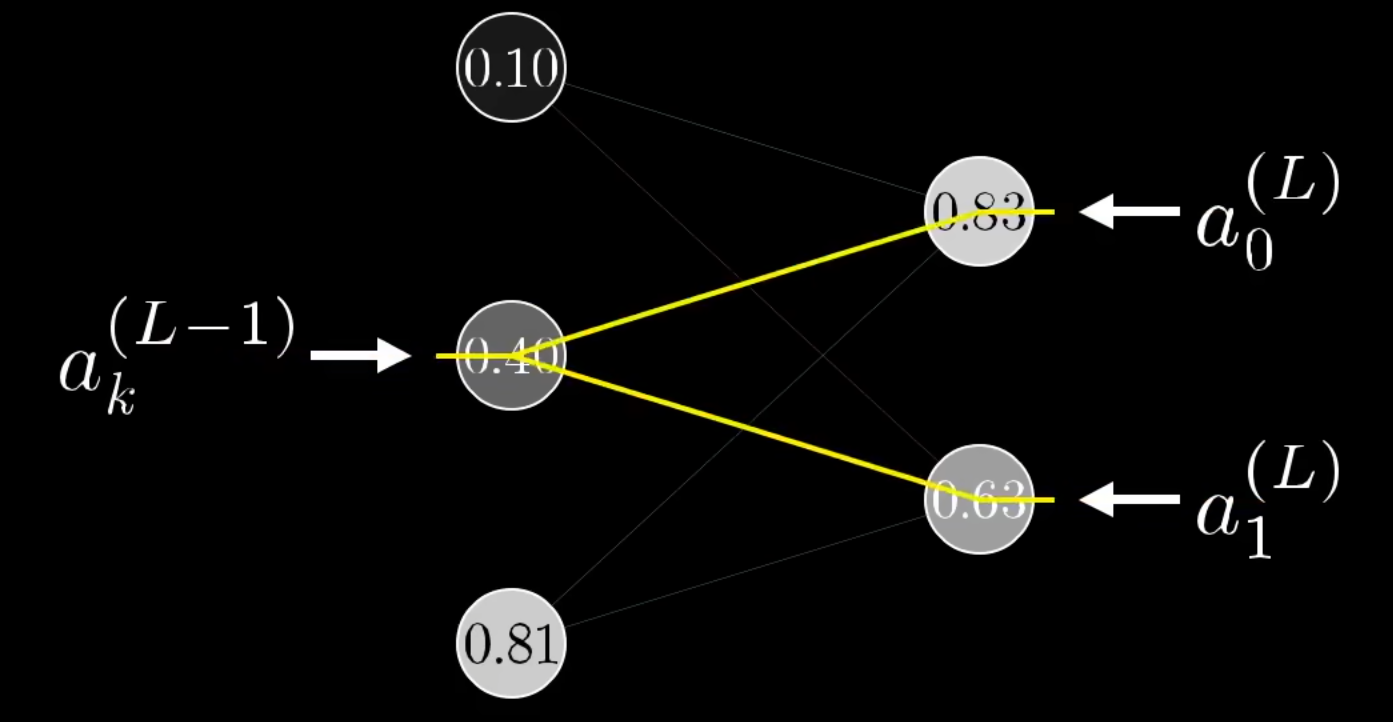
Wenn wir nun die Ableitung bezüglich benötigen, führen wir die Idee fort. Die Berechnung an dieser Stelle ist jedoch komplexer, da jedes Neuron einen Einfluss auf alle Neuronen in allen Folgeschichten hat:

Konkret bedeutet das, dass wir die Summe aller Einflüsse bilden müssen.

Um die Komplexität zunächst so gering wie möglich zu halten, rechnen wir an einem konkreten Beispiel. Uns interessiert die Ableitung :

Etwas allgemeiner erhalten wir die Ableitung also durch Summation der Ableitungen

Bezüglich eines beliebigen Layers

Für ein beliebiges Gewicht in einem beliebigen Layer müssen wir die Summe aller möglichen Einflüsse bilden, dazu benötigen wir für jeden Layer zwischen und der Ausgabeschicht eine Summation. Entsprechend komplex ist der Ausdruck:

Durch Anpassung der Schreibweise von Grant Sandersons an unsere Schreibweise ergibt sich

was zu zeigen war.

Graph View

Mentioned in