Korollar - Satz vom Minimum und Maximum

• Involvierte Definitionen:
  • Minimum
  • Maximum
  • Funktion
  • Stetigkeit
• Referenz: Mathegrundlagen

⠀

Korollar: Satz vom Minimum und Maximum

Sei stetig. Dann gibt es eine Minimalstelle und eine Maximalstelle , sodass

Anmerkung

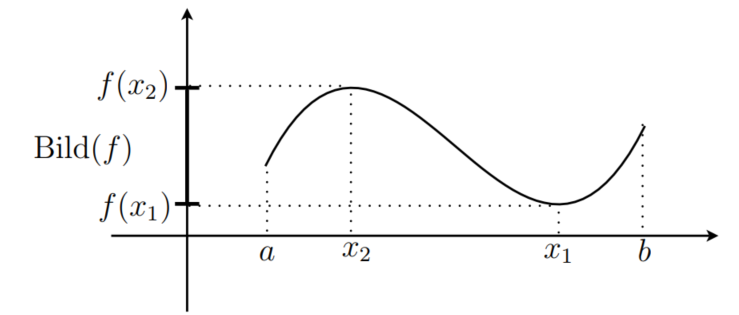
Skizze

Beweis

Teil 1: enthält nur einen Punkt

Gibt es in dem nur einen einzigen Punkt, so haben alle dasselbe Bild und es gilt , wobei wir und beliebig aus wählen können.

Teil 2: ist ein Intervall

Ist ein Intervall, dann gilt mit Satz 15.2.8, dass es sich dabei um ein Abgeschlossenes Intervall handelt, denn

• ist auf einem abgeschlossenen Intervall definiert und
• ist auf diesem Intervall stetig

Sei daher ein abgeschlossenes Intervall mit

• und .

Dann gibt es sodass und .

Da und definitionsgemäß (nämlich ) jeweils das Infimum und Supremum von sind, gilt auch:

und sind also Minimal- und Maximalstelle von .