Definition - Entropie

• Typen:
  • Bedingte Entropie
  • Logistische Kostenfunktion
• Konstrukte:
  • Informationsgewinn
• Involvierte Definitionen:
  • Gelabelter Datensatz
  • Potenzmenge
  • Logarithmus
  • Kardinalität
  • (hier nur empirisch, aber grundsätzlich ein Konstrukt reeller Zufallsvariablen)
• Veranstaltung: EML
• Referenz: @thimm2024 (Abschnitt 2.6.2, Definition 2)

⠀

Definition: Entropie (binär)

Sei binär.
Sei ein gelabelter Datensatz mit .

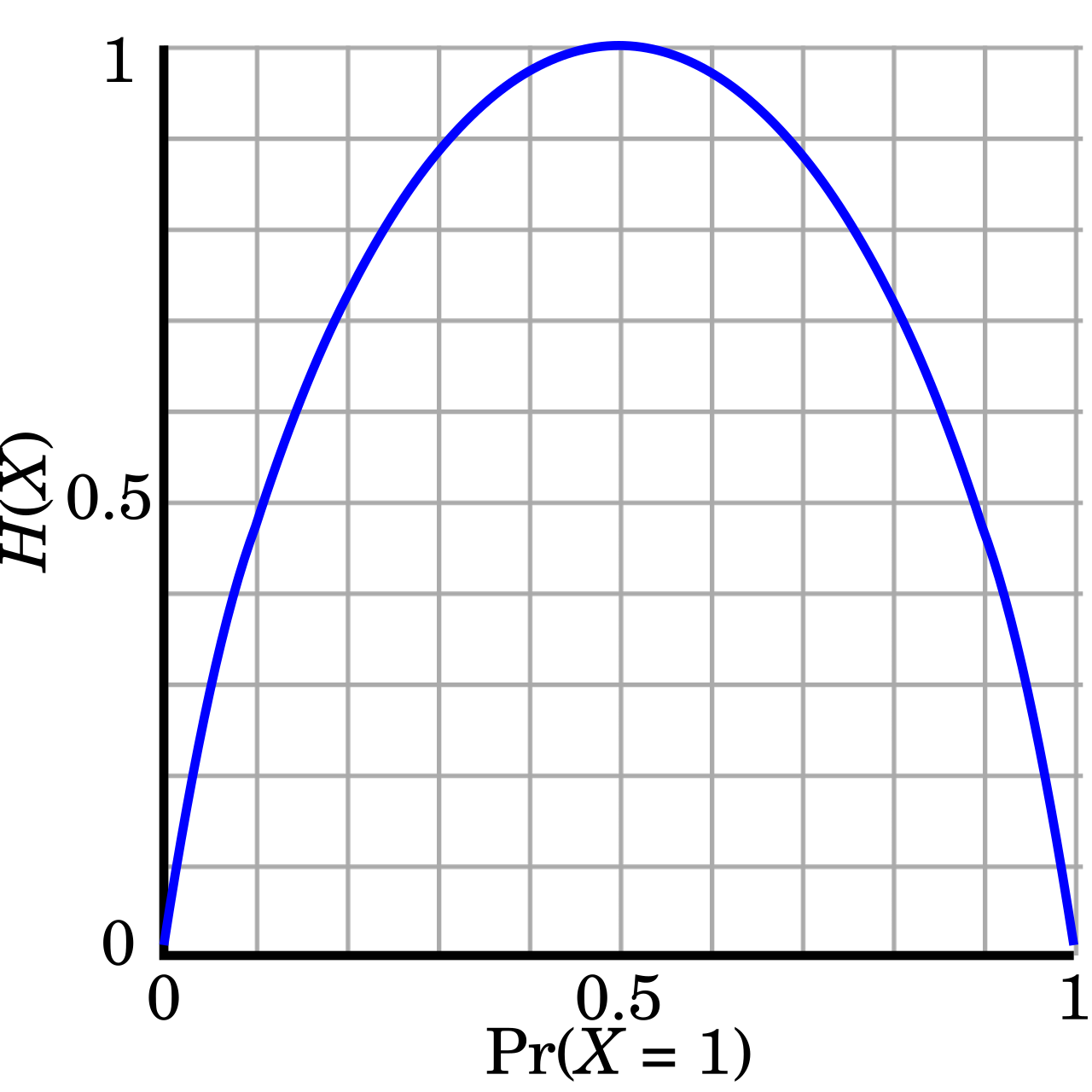
Als binäre Entropie definieren wir die Funktion mit:

Die folgende Abbildung zeigt die Entropie (allerdings mit ) einer binären Zufallsvariable , je nach Variation der Wahrscheinlichkeit . Die Entropie wird maximal, wenn :

Definition: Entropie (allgemein)

Sei mit endlich.
Sei ein gelabelter Datensatz mit .

Als allgemeine Entropie definieren wir die Funktion mit: