Konstrukte:Involvierte Definitionen:Veranstaltung: EiSReferenz: @henze2019
⠀
Definition: Mengensystem der halboffenen Intervalle
Das System (Halbring) aller halboffenen Intervalle
über definieren wir als:
Anmerkung
Wie sieht so ein Intervall eigentlich aus?
Um ein besseres Verständnis der Definition zu entwickeln, versuchen wir sie hier einmal über
zu interpretieren. Laut Definition enthält
alle Intervalle für die
. Dabei sind und zwei Punkte in der Ebene. Wie sehen diese Intervalle nun im Einzelnen aus?
Ändern wir den Blickwinkel ein wenig, können wir erkennen, dass
ein (achsenparalleles) Rechteck ist, dessen linker unterer Eckpunkt von gebildet wird, während den rechten oberen Eckpunkt bildet. Im
-dimensionalen Fall entspricht das Intervall einem (achsenparallelen) Hyperrechteck.
Was ist mit den Randpunkten?
Merke: Die beiden Ränder, die an
anliegen, sind nicht Teil des Intervalls, denn ist ja der offene Randpunkt. Die beiden Ränder hingegen, die an
anliegen, sind Teil des Intervalls, denn ist der abgeschlossene Randpunkt.
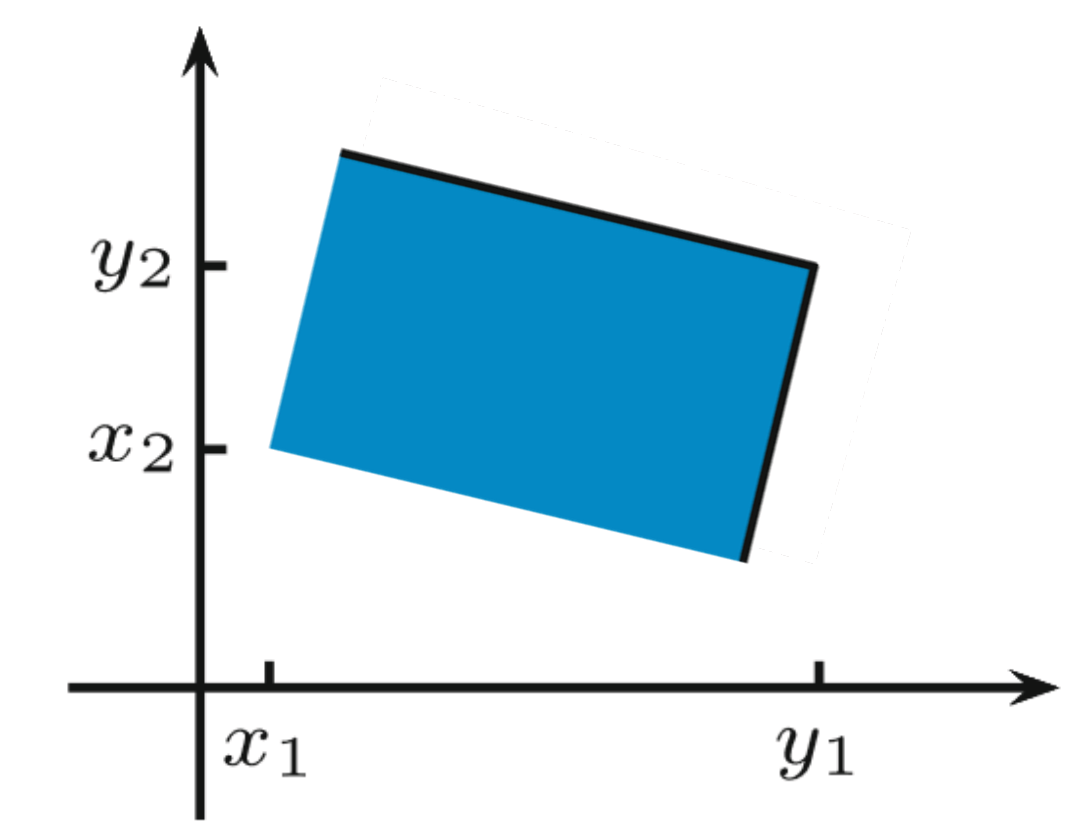
Können wir die Rechtecke eigentlich auch kippen?
Merke: Das Rechteck muss immer achsenparallel sein. Es ist niemals schräg oder gekippt.
Angenommen, wir hätten ein gekipptes Rechteck:
Dann gibt es offensichtlich Punkte
in , für die gilt: . Das ist aber ein Widerspruch zu der Definition mehrdimensionaler Intervalle. Hier muss nämlich für alle gelten, dass .
.png)