Proposition - Vektorprojektion mit dem Skalarprodukt

• Involvierte Definitionen:
  • Skalarprodukt
  • Vektor
• Veranstaltung: MatheDS
• Referenz: @grossmann2023, Video zu Gram-Schmidt

⠀

Proposition: Vektorprojektion mit dem Skalarprodukt

Seien zwei Vektoren.

Mithilfe des Skalarproduktes gilt:

• ist der Projektionsvektor von auf .
• ist der Projektionsvektor von auf .

Identitäten

Im Übrigen gilt:

Anmerkung

Was ist ein Projektionsvektor?

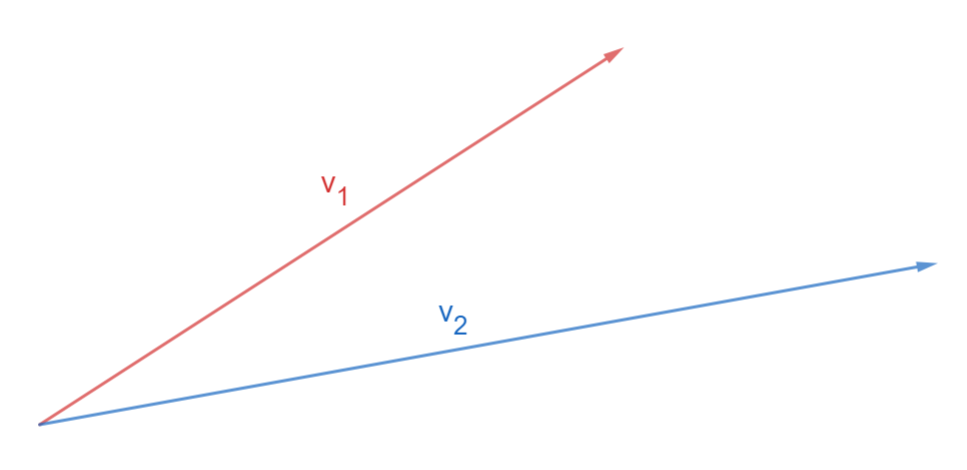
Der Projektionsvektor von auf gibt uns genau die Länge derjenigen Komponente des Vektors , die in die selbe Richtung wie zeigt.

Seien und zwei Vektoren wie folgt:

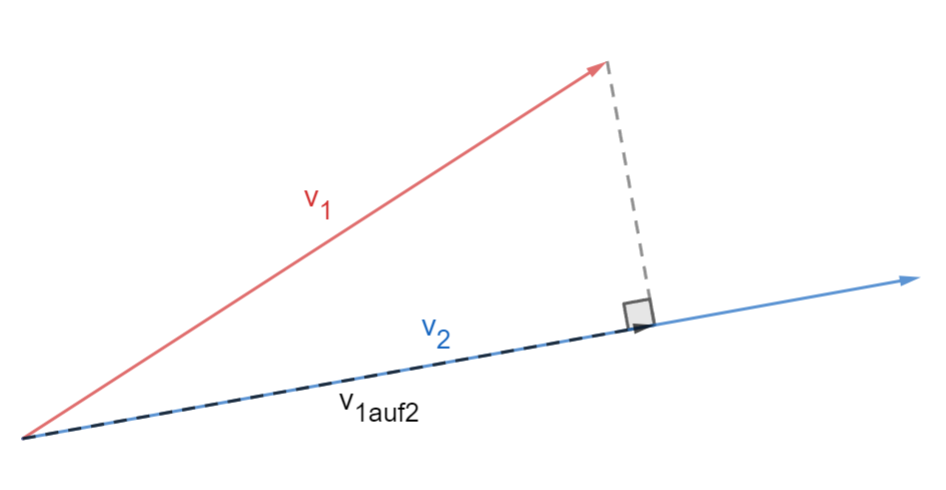
In der folgenden Darstellung ist der Projektionsvektor .

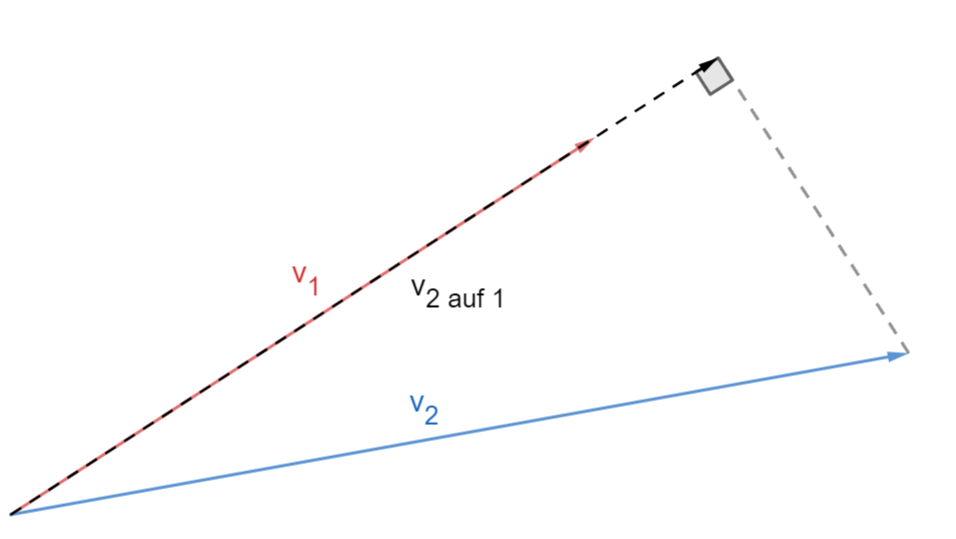
In der folgenden Darstellung ist der Projektionsvektor .