Proposition - Orthogonalvektor

• Involvierte Definitionen:
  • Projektionsvektor
  • Orthogonalität
  • Vektor
• Veranstaltung: MatheDS
• Referenz: Eigener Inhalt

⠀

Proposition: Orthogonalvektor

Seien zwei Vektoren.

Dann gilt:

• ist orthogonal zu .
• ist orthogonal zu .

Anmerkung

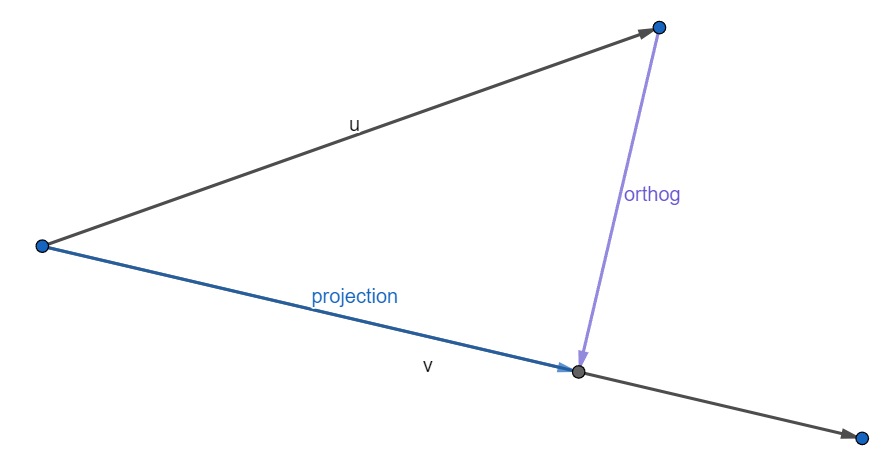
Zusammenhang zwischen Orthogonal- und Projektionsvektor (Orthogonale Entfernung)

Seien zwei Vektoren.
Sei der Projektionsvektor von auf .
Sei der orthogonale Vektor.

Dann gilt:

ist genau der Vektor, der von aus auf den Projektionsvektor zeigt und ist genau der Abstand zwischen dem Projektionsvektor und .

In anderen Worten: gibt an, wie weit von orthogonal entfernt ist:

Beweis

Ohne Beschränkung der Allgemeinheit betrachten wir hier den Fall der Orthogonalität zu .

Wir wissen bereits, dass

der Projektionsvektor von in Richtung von ist. Das heißt: gibt uns genau die Länge derjenigen Komponente des Vektors , die in die selbe Richtung wie zeigt.

Das bedeutet aber auch: ziehen wir von ab, so zeigt der neue Vektor überhaupt nicht mehr in die Richtung von , denn die gesamte “in Richtung zeigende Komponente” haben wir ja aus entfernt.

Damit sind und genau orthogonal, was zu zeigen war.