Proposition - Skalar ist Eigenwert iff Skalar ist Nullstelle des charakteristischen Polynoms

• Involvierte Definitionen:
  • Eigenwert
  • Quadratische Matrix
  • Charakteristisches Polynom einer Matrix
  • Determinante
• Veranstaltung: AlMa
• Referenz: @herzogWiSe22

⠀

Proposition: Bestimmung von Eigenwerten durch charakteristisches Polynom

Sei eine quadratische Matrix.
Sei ein Skalar.
Sei das charakteristische Polynom von .

Dann gilt:

Beweis

Da gilt, dass

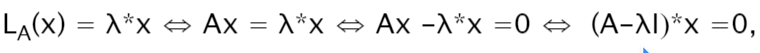
folgt, dass sein muss, denn soll ja ungleich null sein. Das ist aber nur möglich, wenn die Spalten von linear abhängig sind. Wären sie linear unabhängig, dann wäre , damit wäre invertierbar es gäbe kein , dass das LGS löst.

Der Rest folgt mit Proposition - Spalten sind linear abhängig gdw Determinante ist Null