Algorithmus - FPTree-Algorithmus

• Konstrukte/Folgerungen:
  • Konditionierte Datenbasis
  • FPGrowth-Algorithmus
• Involvierte Definitionen:
  • FP-Baum
  • FP-Knoten
  • Transaktionsdatensatz
• Veranstaltung:
  • EML
  • DM
• Referenz:
  • @thimm2024 (Abschnitt 3.3.3)
  • @valdes2025 (p. 104 ff.)

⠀

Algorithmus: FPTree

Sei eine Itemmenge.
Sei ein Transaktionsdatensatz über .

Als FPTree-Algorithmus zur Erstellung eines FP-Baumes bezeichnen wir folgenden Algorithmus:

---

Eingabe: Transaktionsdatensatz ,
Ausgabe: FP-Baum für

// Liste der häufigen Items, absteigend nach Häufigkeit sortiert (also das häufigste Item zuerst)

for do
// die Items aus nach der Ordnung von

while do
if hat kein Kind für then
Sei ein neuer Knoten

Sei

return

Anmerkung

Beispiel: FPTree in Vorbereitung auf FPGrowth

Um den FPTree-Algorithmus im weiteren Verlauf auch für den FPGrowth-Algorithmus nutzen zu können, müssen wir uns neben dem Baum selbst auch noch merken, in welcher Reihenfolge die Knoten angelegt wurden.

Um das Vorgehen klar zu machen, bearbeiten wir ein Beispiel.

Sei die minimale Anzahl an Items gegeben mit .
Sei folgende Transaktionsdatenbank gegeben:

TID	Items	TID	Items	TID	Items	TID	Items

Wir bestimmen nun zunächst für jedes Item die Häufigkeit. Einerseits, um Items mit zu geringer Häufigkeit schon im Vornherein auszuschließen. Andererseits, um die sortierte Liste zu bilden.

Itemset
Häufigkeit	5	5	6	2	4

Offensichtlich, ist keines der Items auszuschließen, da sie alle die Mindestanzahl erreichen. Für erhalten wir nun als - wobei die Reihenfolge von und auch getauscht sein dürfte, da beide gleich häufig auftreten.

Wir beginnen nun mit der ersten Transaktion . Beim Zeichnen des Baumes hangeln wir uns immer an der Liste entlang und erhalten:

Zusätzlich verbinden wir die Elemente der Liste über einen Pfeil mit den erstellten Elementen im Baum.

---

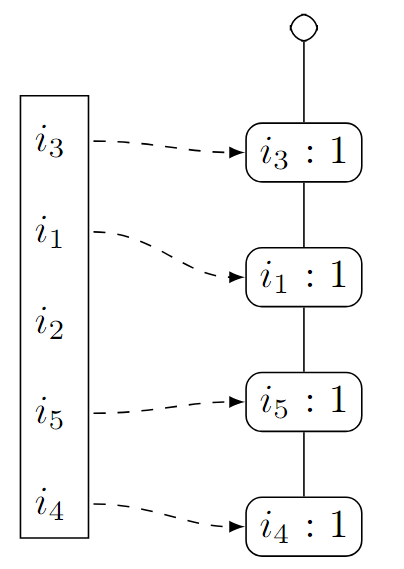
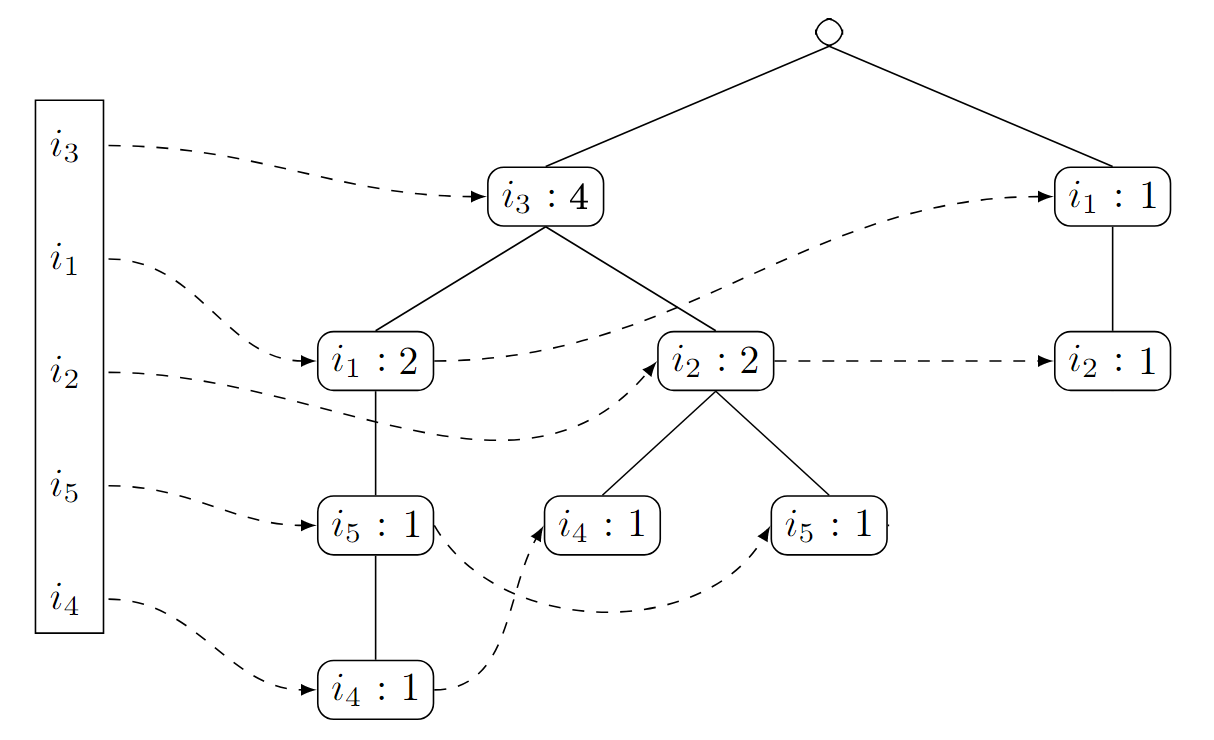
Wir fahren fort mit der zweiten Transaktion . Sie startet ebenfalls mit (weshalb wir den Zähler erhöhen), enthält aber nicht, weshalb wir einen neuen Kindknoten zu hinzufügen müssen:

Das Element ist neu - wir ziehen wieder eine gestrichelte Linie von der Liste zu dem Knoten . Außerdem haben wir eine neue Knoten-Instanz von hinzugefügt. Wir ziehen daher eine gestrichelte Linie von dem letzten Knoten von zu der neuen Knoten-Instanz.

---

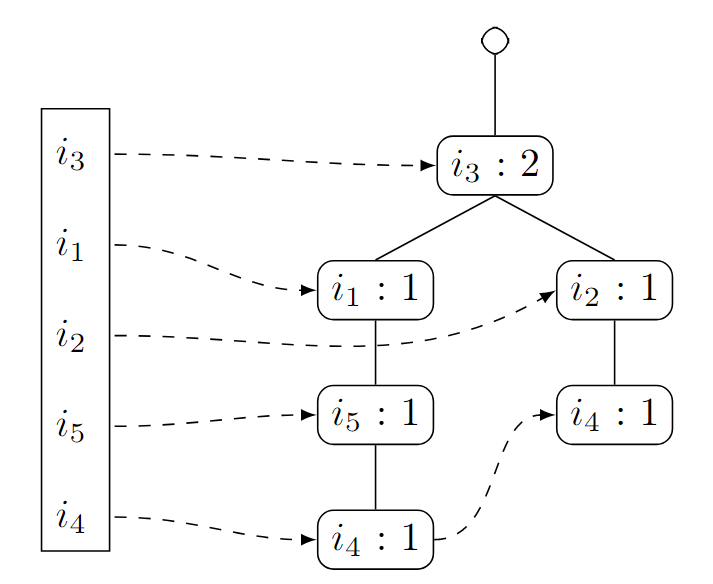
Wir fahren fort mit der dritten Transaktion . Sie enthält nicht, weshalb wir einen neuen Knoten anlegen. Wieder orientieren wir uns an und starten daher mit . Wir erhalten:

Die Verbindungen zu den neuen Knoten fügen wir entsprechend ebenfalls hinzu.

---

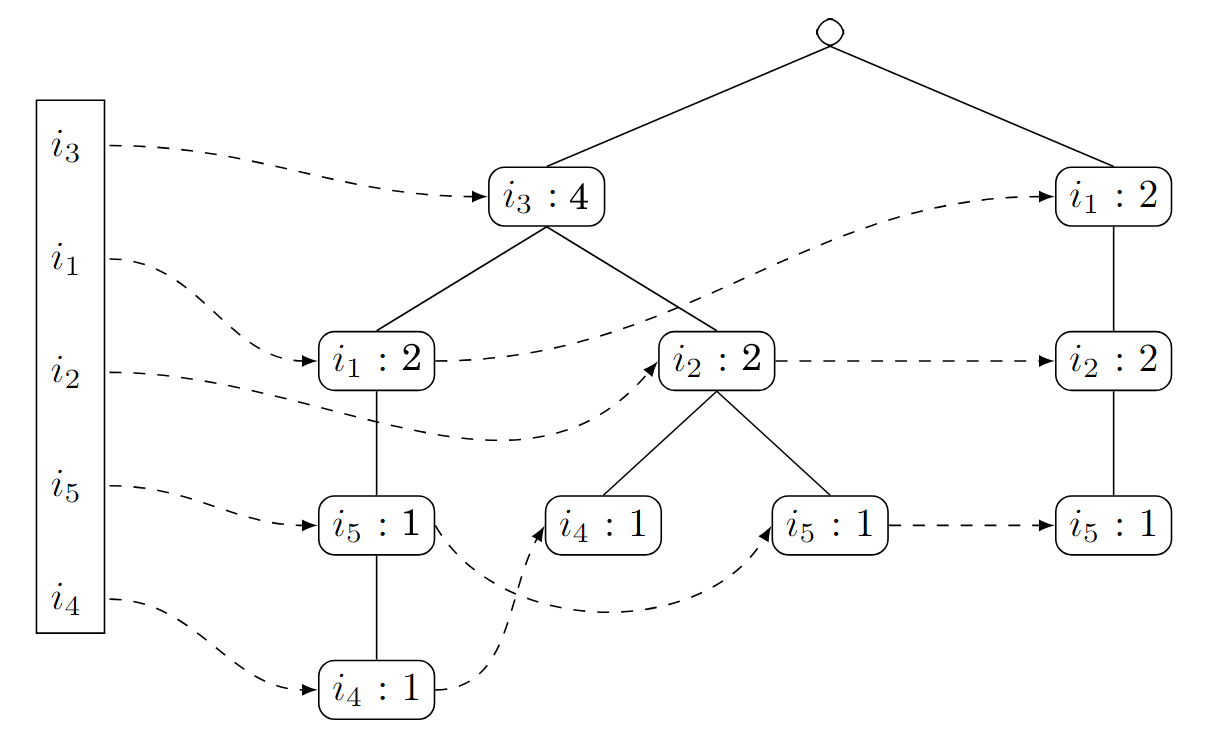
Wir fahren fort mit der vierten Transaktion . Hier müssen wir nur die Zähler in und erhöhen:

---

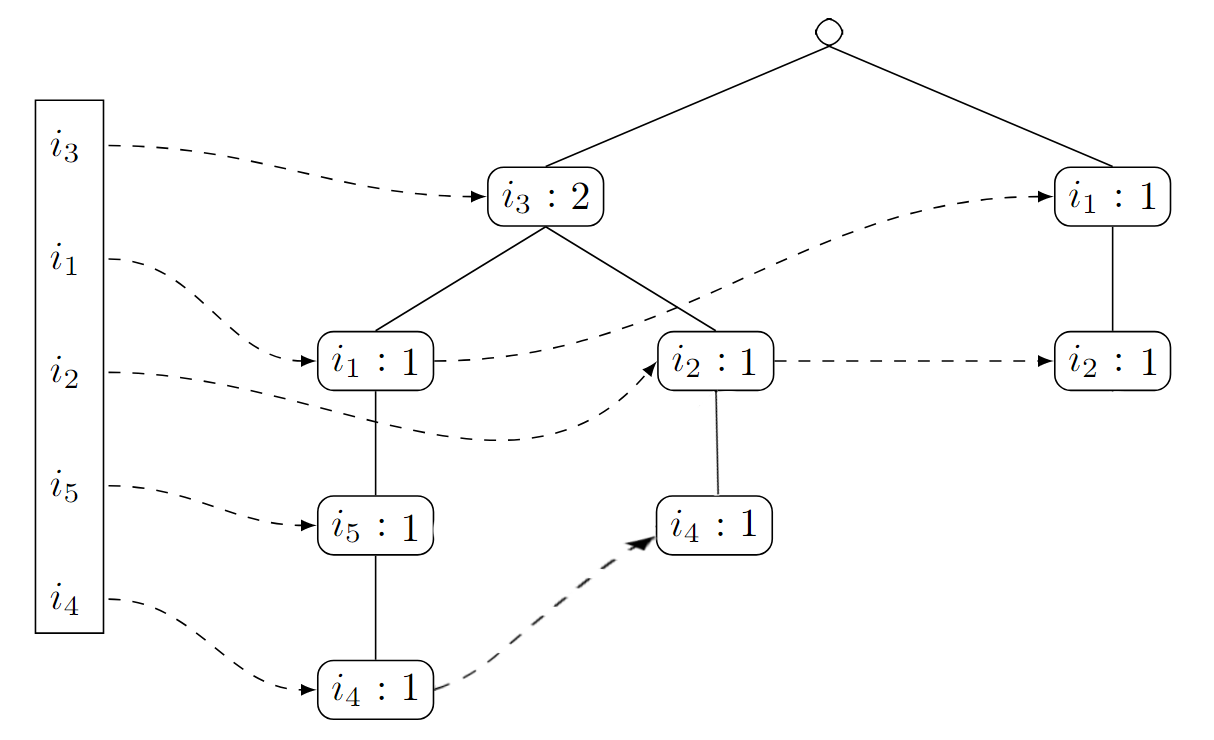
Wir fahren fort mit der fünften Transaktion . Wir folgen dem Pfad und erkennen, dass wir einen neuen Knoten für erzeugen müssen. Wir erhalten:

---

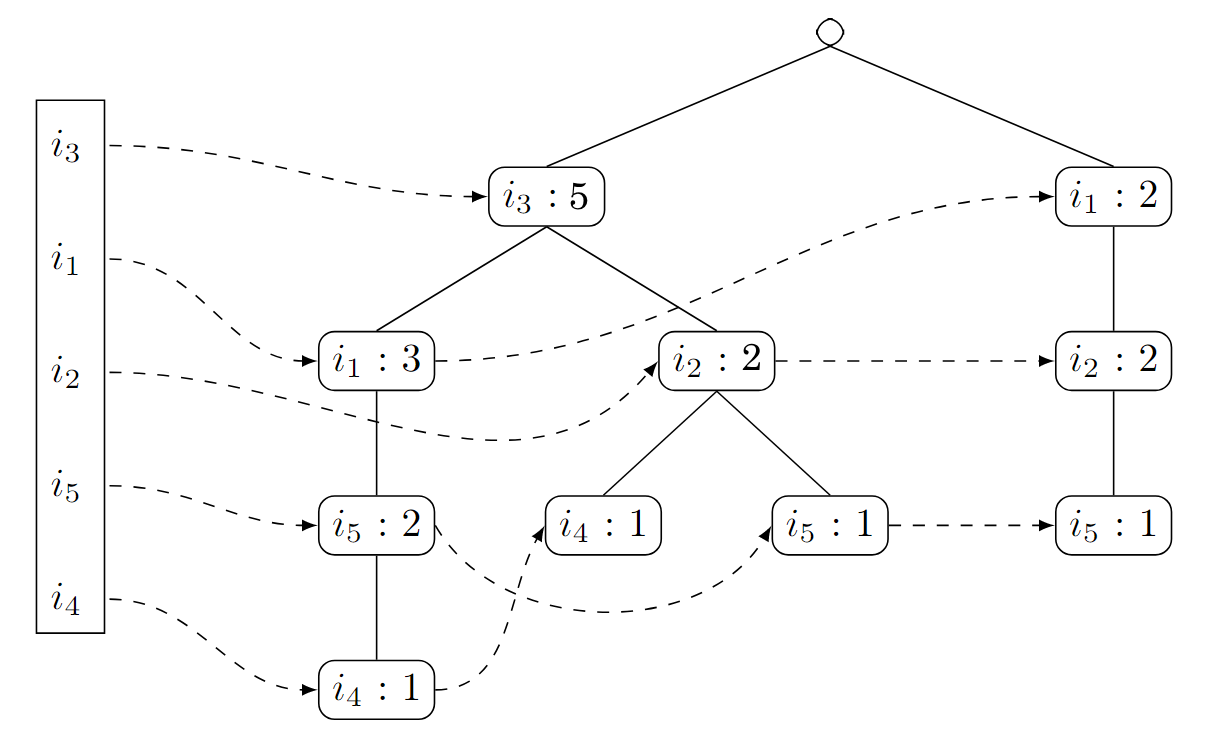
Wir fahren fort mit der sechsten Transaktion . Wir folgen dem Pfad und konstruieren einen weiteren Knoten , den wir wieder mit dem letzten Vorgänger-Knoten verbinden:

---

Wir fahren fort mit der siebten Transaktion . Hier müssen wir nur die Zähler in , und erhöhen:

---

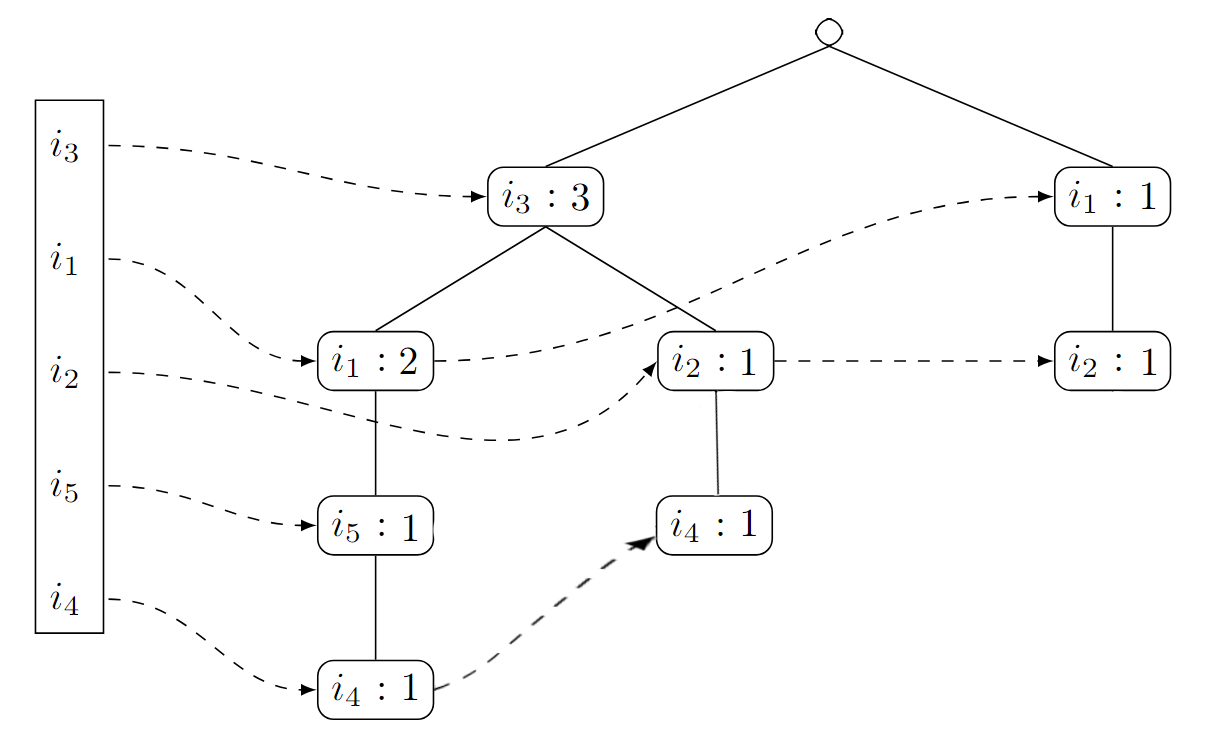
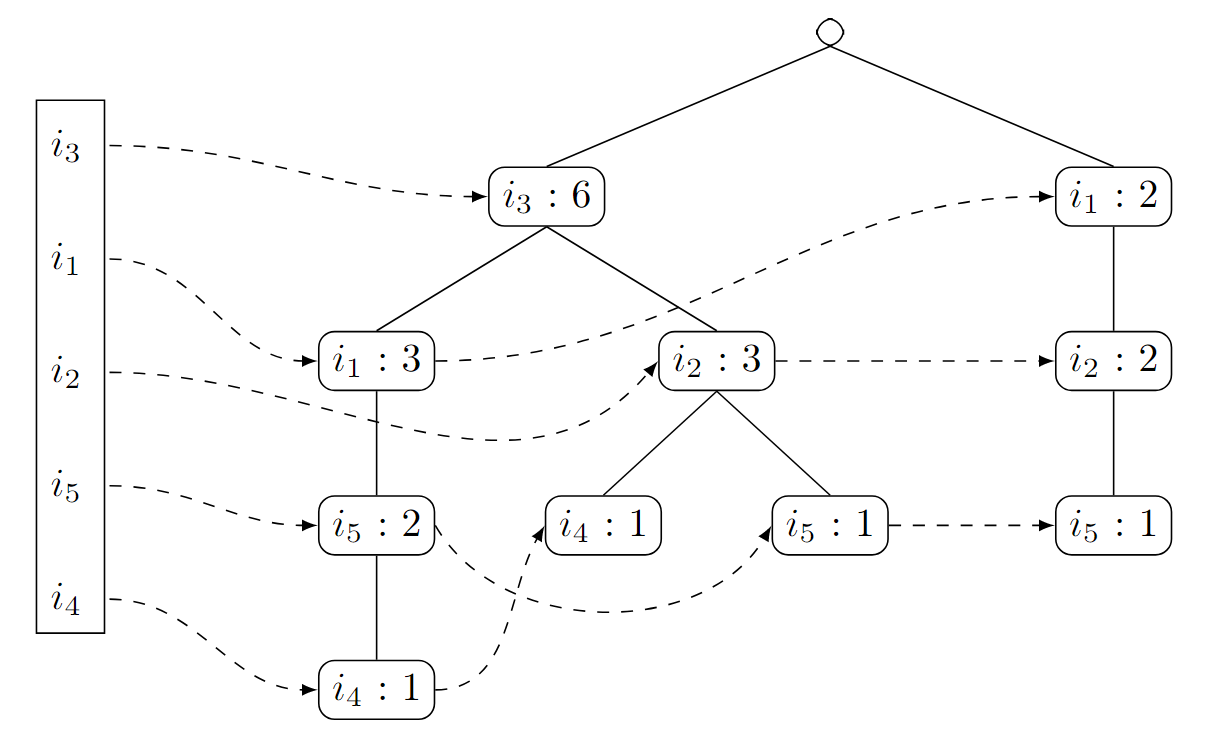
Wir fahren fort mit der achten und letzten Transaktion . Hier müssen wir nur die Zähler in und erhöhen und sind fertig: