Algorithmus - FPGrowth-Algorithmus

• Bewiesen durch:
  • Charakterisierung der FrequentPattern-Funktion
• Involvierte Definitionen:
  • Transaktionsdatensatz
  • FPTree-Algorithmus
  • FrequentPattern-Funktion
  • Konditionierte Datenbasis
• Veranstaltung:
  • EML
  • DM
• Referenz:
  • @thimm2024 (Abschnitt 3.3.3)
  • @han2000

⠀

Algorithmus: FPGrowth-Algorithmus

Sei eine Itemmenge.
Sei ein Transaktionsdatensatz über .

Als FPGrowth-Algorithmus zum Auffinden häufiger Itemsets bezeichnen wir folgenden Algorithmus:

---

Eingabe: Transaktionsdatensatz ,
Ausgabe:

if besteht aus einem einzigen Pfad then
Menge aller nicht-leeren Teilmengen von Elementen in
else
for do


return

Anmerkung

FPGrowth in der Praxis

Um das händische Vorgehen möglichst klar zu machen, bearbeiten wir ein Beispiel. Sei die minimale Anzahl an Items gegeben mit .
Sei folgende Transaktionsdatenbank gegeben:

TID	Items	TID	Items	TID	Items	TID	Items

Wir bestimmen nun zunächst für jedes Item die Häufigkeit. Einerseits, um Items mit zu geringer Häufigkeit schon im Vornherein auszuschließen. Andererseits, um die sortierte Liste zu bilden.

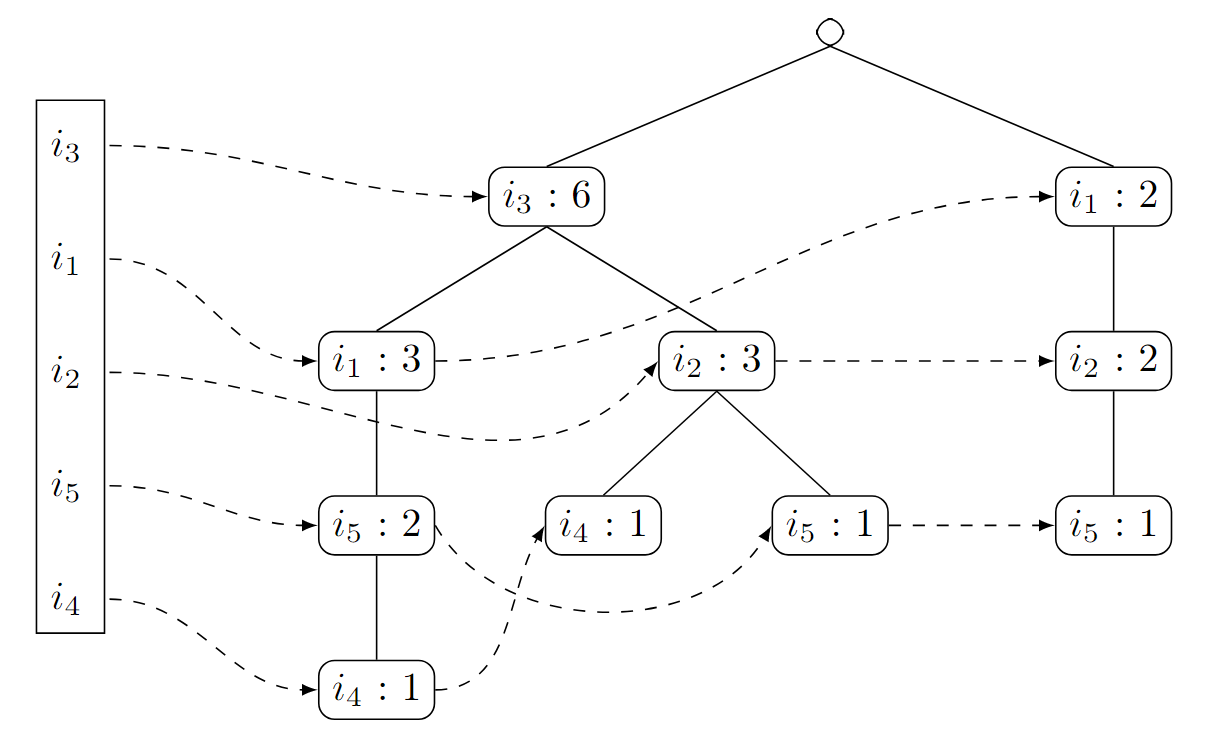
Itemset
Häufigkeit	5	5	6	2	4

Anschließend führen wir den FPTree-Algorithmus durch. In diesem Fall erhalten wir nach acht Iterationen den folgenden FP-Baum:

---

Jetzt steigen wir richtig in den FPGrowth-Algorithmus ein. Hierzu wählen wir zunächst das letzte Element aus unserer sortierten Liste - in diesem Fall . Jetzt bilden wir die konditionierte Datenbasis (im Skript zu Datamining auch Musterbasis .

Dabei helfen uns die gestrichelten Pfeile:

• Wir folgen dem Pfeil zunächst zu dem ersten Knoten und können die folgenden Vater-Knoten ablesen: .
• Folgen wir dem gestrichelten Pfeil weiter, erhalten wir .

Es gilt also: . Für müssen wir jetzt einen neuen FP-Baum erzeugen. Dazu schauen wir zunächst, welche Elemente die Grenze erreichen - in diesem Fall ist das lediglich . Wir erhalten also einen FP-Baum mit nur einem Knoten.

Wir erhalten hier also als häufige Itemsets.

---

Wir machen mit dem zweit-niedrigsten Knoten weiter - das ist in diesem Fall . Um die konditionierte Datenbasis zu bilden, folgen wir wieder den Pfeilen und erhalten:

• (tritt zwei mal auf, weil die Multiplizität von am ersten verbundenen Knoten beträgt)

Wir erhalten also . Wir schauen jetzt wieder, welche Items häufig sind, um einen entsprechenden FP-Baum für zu konstruieren.

Itemset
Häufigkeit	3	2	3

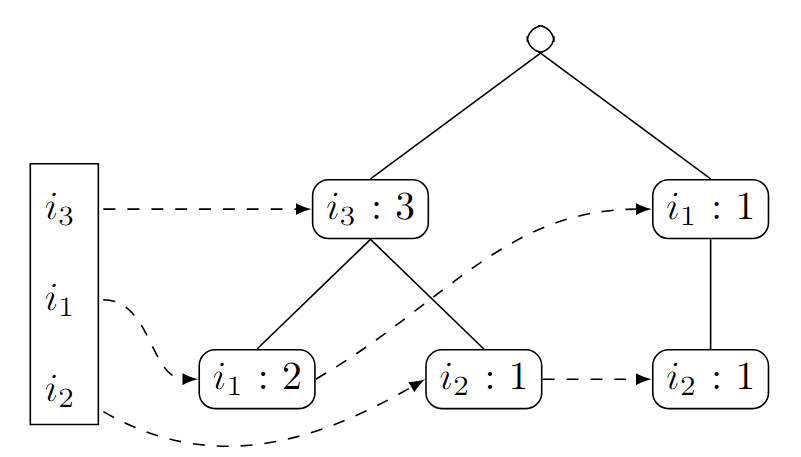
Wir merken uns daher schon mal die Kombinationen als häufig vor.

Wir führen nun den FPTree-Algorithmus aus und erhalten:

Für diesen Teilbaum führen wir nun wieder FPGrowth durch. Wir beginnen mit :

Hiervon ist kein Element häufig, da sie jeweils nur einmal vorkommen, aber es gilt .

Weiter mit :

Hier ist häufig, wir erhalten also .

Für haben wir schließlich .

Wir können den Teilbaum also abschließen mit als Ergebnis des Teilbaums für .

Das Gesamtergebnis für ist daher: .

---

Wir machen mit dem dritt-niedrigsten Knoten weiter - das ist in diesem Fall . Um die konditionierte Datenbasis zu bilden, folgen wir wieder den Pfeilen und erhalten:

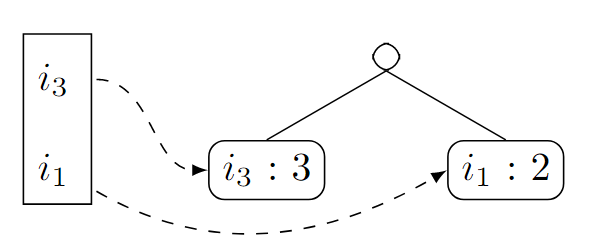
Bei und handelt es sich also um häufige Mengen (da sie jeweils mindestens zwei Mail auftreten).

Das ergibt dann folgenden FP-Baum:

Aus dem können wir aber nichts weiter ablesen. Wir erhalten daher als häufige Mengen .

---

Weiter geht es mit . Um die konditionierte Datenbasis zu bilden, folgen wir wieder den Pfeilen und erhalten:

Als häufige Menge erhalten wir also

---

Für den letzten Knoten, , lässt sich jetzt keine Obermenge mehr konstruieren, daher sind wir fertig.

Als häufige Mengen haben wir jetzt zusammengefasst:

• 1-elementige häufige Mengen:
• 2-elementige häufige Mengen:
• 3-elementige häufige Mengen: