Typen:Beispiele:Involvierte Definitionen:Veranstaltung: IRReferenz: @wagenpfeil2024 (KE3. p. 10 ff.)
⠀
Definition: Erweitertes Boolesches Modell
Als erweitertes boolesches Modell bezeichnen wir ein Best-Match-Modell, das die Logik des booleschen Retrievals mit der graduellen Bewertung des Vektorraummodells verbindet.
Wie im Vektorraummodell erhält jedes Dokument für jeden Term ein Gewicht
das beschreibt, wie stark der Term
in dem Dokument ausgeprägt ist. Der Gewichtsvektor eines Dokumentes lautet dann wobei
die Anzahl der Terme sei. Boolesche Anfragen wie
oder , wobei zwei Terme seien, bleiben zulässig. Im Unterschied zum klassischen booleschen Modell werden die Operatoren jedoch nicht binär, sondern weich interpretiert. Eine Aggregationsfunktion bestimmt, wie gut ein Dokument das Idealverhalten des jeweiligen Operators (
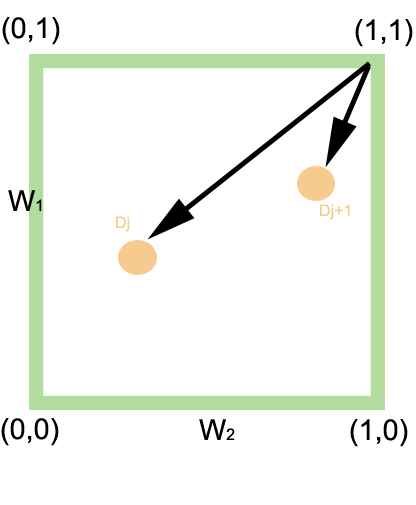
bzw. ) erfüllt. Eine AND-Abfrage wird von Dokumenten umso besser erfüllt, je höher ihre Gewichte in den beteiligten Termdimensionen ausfallen. Geometrisch entspricht das einer Annäherung an den Punkt
. Im zweidimensionalen Beispiel erhält das Dokument
einen höheren Score als , weil sein Abstand zum Punkt geringer ist:
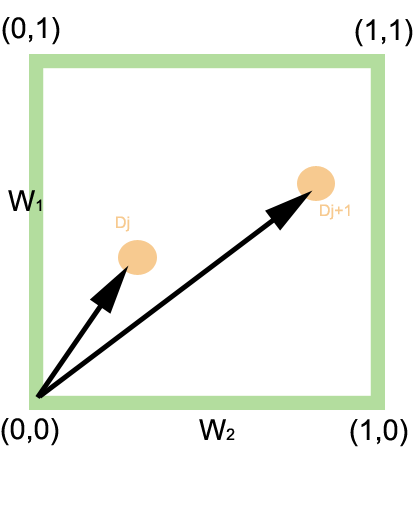
Eine OR-Abfrage wird von Dokumenten umso besser erfüllt, je mehr der beteiligten Termdimension hohe Gewichte aufweisen. Geometrisch entspricht das einer größeren Entfernung vom Ursprung
. Im zweidimensionalen Beispiel erhält das Dokument
einen höheren Score als , weil sein Abstand zum Ursprung größer ist:
Anmerkung
Achtung: Modell-Familie
Das Erweiterte Boolesche Modell ist nicht ein Modell, sondern eine Modell-Familie. Es können unterschiedliche Maße gewählt werden. Die beiden geometrischen Beispiel nutzen zwar die euklidische Distanz - das sind aber eben nur Beispiele. Es können hier auch ganz andere Funktionen genutzt werden.