Algorithmus - Inverse Diskrete Wavelet-Transformation mit Haar-Wavelet

• Konstrukte/Folgerungen:
  • DWT mit Haar-Wavelet
• Involvierte Definitionen:
• Veranstaltung: DM
• Referenz: @valdes2024 (p. 78 ff.)

⠀

Algorithmus: Inverse Diskrete Wavelet-Transformation mit Haar-Wavelet (Iterativ)

Als Inverse Diskrete Wavelet-Transformation mit Haar-Wavelet bezeichnen wir ein Verfahren zur Umkehrung einer DWT und zur Wiederherstellung der ursprünglichen Zeitreihe.

Sei eine DWT mittels Haar-Wavelet gegeben durch

Dann erhalten wir die ursprüngliche Zeitreihe iterativ, indem wir die Detailwerte der aktuellen Stufe abwechselnd zu den Approximationswerten der vorangegangenen Stufe addieren oder subtrahieren:

• Iteration 1 (Approx: ; Detail: )
• Iteration 2 (Approx: ; Detail: )
  • Teil 1 (Approx: ; Detail: )
  • Teil 2 (Approx: ; Detail: )
• Iteration 3 (Approx: ; Detail: )
  • Teil 1 (Approx: ; Detail: )
  • Teil 2 (Approx: ; Detail: )
  • Teil 3 (Approx: ; Detail: )
  • Teil 4 (Approx: ; Detail: )

wobei jeweils für den -ten Approximationswert der aktuellen Stufe steht.

Als Ergebnis erhalten wir und sind fertig.

Algorithmus: Inverse Diskrete Wavelet-Transformation mit Haar-Wavelet (Summe von Basen)

Als Inverse Diskrete Wavelet-Transformation mit Haar-Wavelet bezeichnen wir ein Verfahren zur Umkehrung einer DWT und zur Wiederherstellung der ursprünglichen Zeitreihe.

Sei eine DWT mittels Haar-Wavelet gegeben durch

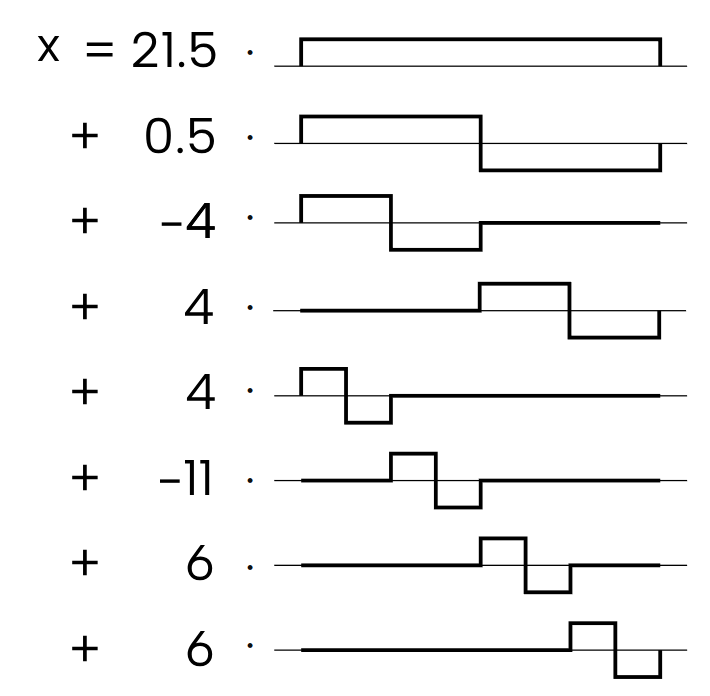
Nach Definition der DWT lässt sich die ursprüngliche Zeitreihe als Summe von Box-Basen darstellen. Die diskrete Wavelet-Transformation wandelt diese Darstellung in eine Summe von Wavelet-Basen um.

Für eine DWT mit Ergebnis

erhalten wir die Ausgangsfolge also durch

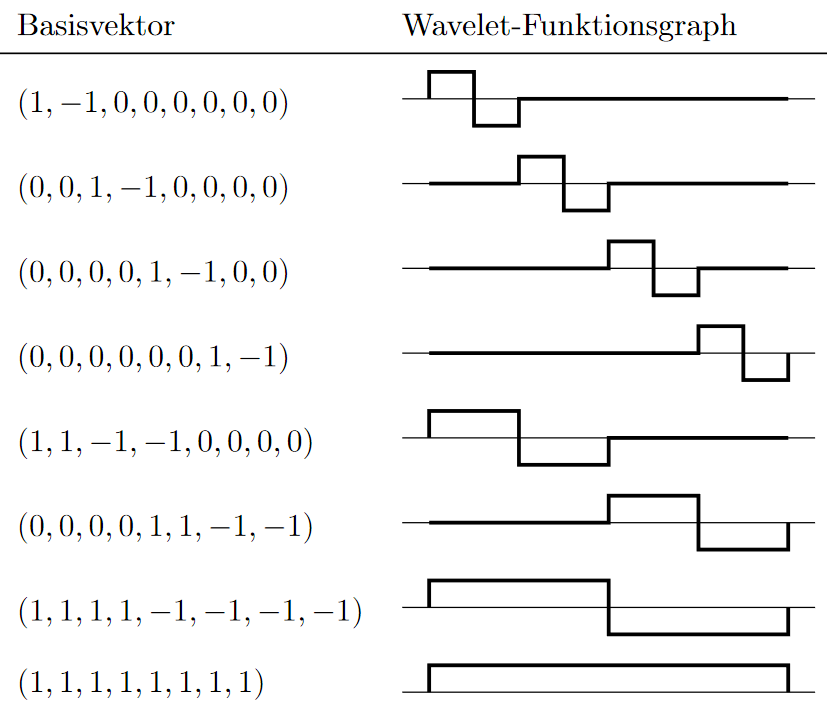
Die Box- und Wavelet-Basen können wir nun nicht nur visuellen sondern auch als numerische Vektoren auffassen mit:

Um zu erhalten, müssen wir jetzt nur noch die Summe der Koeffizienten mit dem jeweiligen Basisvektor bilden.

wobei der jeweilige Koeffizient der DWT, der jeweilige Basisvektor seien und die Länge des DWT-Ergebnisvektors sei.

Da das händische Addieren vieler Vektoren anstrengend ist, berechne ich die jeweiligen Teile von direkt¹.

Wir erhalten also wieder

und sind fertig.

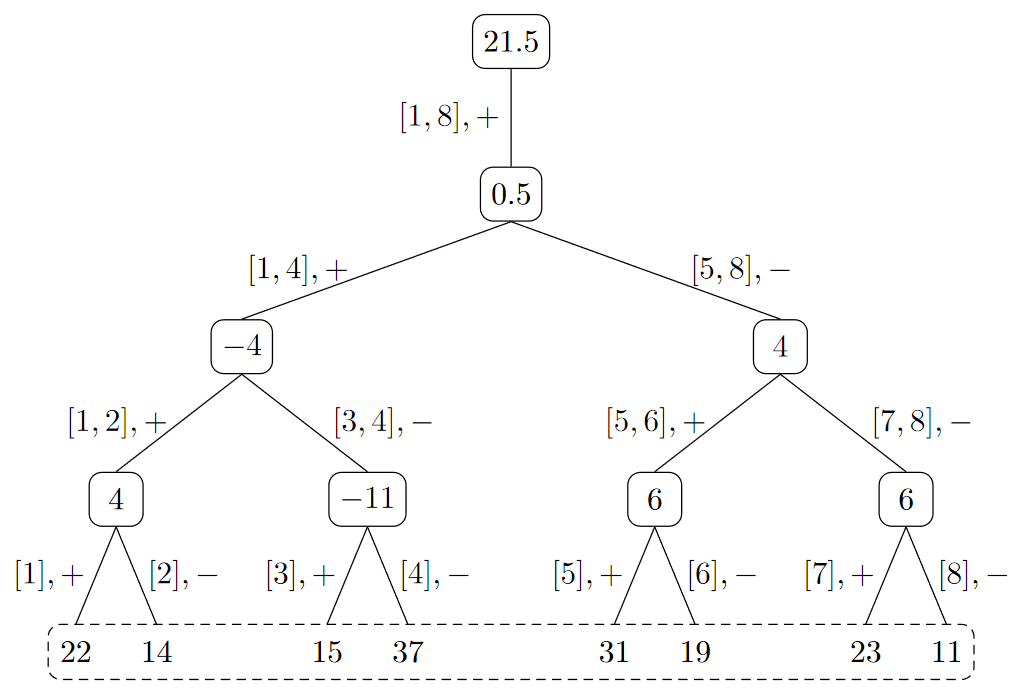
Baumdarstellung

Die IDWT mittels Summierung der Basen lässt sich auch als Baum darstellen druch:

Footnotes

1. Das geht besonders effizient, wenn man zunächst einmal die Gleichungen nach dem Schema aufstellt: erst überall dann bei den ersten vier , bei den letzten vier usw. ↩