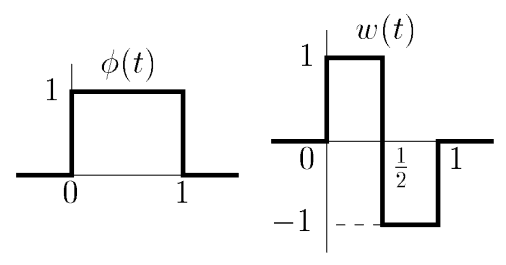Algorithmus - Diskrete Wavelet-Transformation mit Haar-Wavelet

• Konstrukte/Folgerungen:
  • IDWT mit Haar-Wavelet
• Generalisierungen:
  • Diskrete Wavelet-Transformation
• Involvierte Definitionen:
• Veranstaltung: DM
• Referenz:
  • @valdes2024 (p. 78 ff.)
  • @stollnitz1994
  • @owens1997 (Lecture #1 und #2)
  • Wavelets: a mathematical microscope by Artem Kirsanov
  • The Wavelet Tutorial by Robi Polikar, insb. Part 4
  • Wikipedia

⠀

Algorithmus: Diskrete Wavelet-Transformation mit Haar-Wavelet

Als Diskrete Wavelet-Transformation mit Haar-Wavelet definieren wir ein iteratives Vorgehen, bei dem wir eine Zeitreihe mit Einträgen in ein Array von Approximations- und Wavelet-Werten zerlegen.

Zur Durchführung der Zerlegung nutzen wir die Skalierungs-Funktion sowie die Wavelet-Funktion des Haar-Wavelets:

wobei für bspw. gelte, dass

Das iterative Vorgehen ist dann wie folgt:

• Iteration 1
  • Approximationswerte mittels auf Basis der originalen Zeitreihe berechnen
  • Detailwerte mittels auf Basis der originalen Zeitreihe berechnen
• Iteration 2
  • Approximationswerte mittels auf Basis von berechnen
  • Detailwerte mittels auf Basis von berechnen
• Iteration
  • Approximationswerte mittels auf Basis von berechnen
  • Detailwerte mittels auf Basis von berechnen

Sobald das Ergebnis in Schritt nur noch einen einzigen Approximationswert und einen Detailwert enthält, endet der Algorithmus. Das Ergebnis ist dann das Array¹:

äää

Herleitung und Beispiel

Durchführung der diskreten Wavelet-Transformation

Für die Durchführung der DWT gibt es einige unterschiedliche Herangehensweisen und Formulierungen.

Um uns das Leben einfach(er) zu machen, leiten wir den Algorithmus auf Basis des verhältnismäßig simplen Haar-Wavelets her.

Die Grundidee ist, dass Wavelets nicht alleine, sondern sich immer mittels eines Paares aus Wavelet-Funktion, , und Scaling-Funktion, , definiert werden.

Für das Haar-Wavelet gilt:

Dabei entspricht der “Box-Funktion” und ist das typische Haar-Wavelet²:

Da beide Funktionen nur auf dem Intervall einen Wert ungleich haben, werden sie oft auch in Vektorform dargestellt, nach dem Schema

Wir teilen an dieser Stelle durch , um das Ergebnis zu normieren. Würden wir durch teilen, wären die Filter sogar orthonormal (- was für uns an dieser Stelle nicht so wichtig ist, in Software-Paketen aber oft gemacht wird).

In der Literatur werden und auch als

• : Low-Pass-Filter oder Approximation-Filter
• : High-Pass-Filter oder Detail-Filter

bezeichnet.

Bei der kontinuierlichen Wavelet-Transformation können wir uns dynamisch aussuchen, auf welche Frequenzen wir eine Zeitreihe untersuchen wollen.

Bei der diskreten Wavelet-Transformation haben wir diesen Luxus nicht. Stattdessen zerlegen wir eine Zeitreihen in eine feste Anzahl “skalierter Wavelets” in unterschiedlichen Breiten, die in Summe wieder die Ausgangs-Zeitreihe ergeben. Konkret berechnen wir die Koeffizienten, die für das Skalieren der Wavelets benötigt werden.

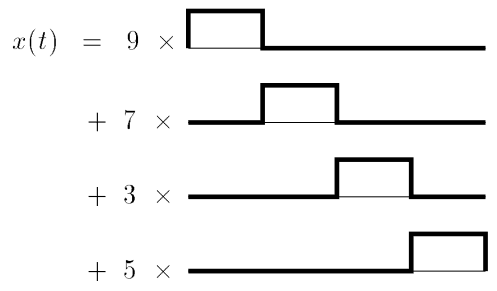
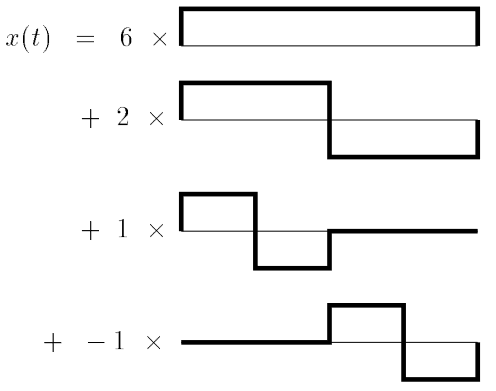
Wir starten mit einem Beispiel¹:

Diese Funktion können wir zunächst in der “Box-Basis” darstellen durch¹:

Visualisieren wir die Summe, erhalten wir

Wie können wir die Zerlegung in der Box-Basis nun in Wavelets unterschiedlicher Frequenz zerlegen? Iterativ! In jeder Iteration berechnen wir zwei Gruppen von Werten:

• Geglättete “Restfrequenzen” (in der Literatur oft Approximationswerte)
• Wavelet-Koeffizienten (in der Literatur oft Detailwerte)

Und diese beiden Gruppen erhalten wir, indem wir unseren Low-Pass Filter sowie unseren High-Pass Filter auf die Sequenz anwenden.

Dabei schieben wir unsere Filter wie ein sliding window über die Zeitreihe, wobei wir immer ganze “Datenpaare” betrachten, also zuerst das Paar und dann das Paar . In der Literatur wird dieses Vorgehen des Verschiebens über ganze Datenpaare auch als Subsampling bezeichnet.

Machen wir das also einmal für unseren Low-Pass- und High-Pass-Filter:

• Low-Pass (Approximationswerte)
• High-Pass (Detailwerte):

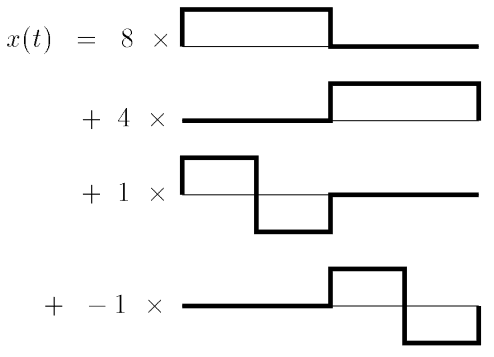
Mit den gefundenen Werten können wir jetzt nicht mehr nur in der Basis , sondern - übergreifend - in und darstellen durch¹:

Dabei umspannen sowohl als auch das gesamte ursprüngliche Signal jedoch mit halbierter Sampling Rate (jeweils nur noch zwei Samples statt ursprünglich 4).

Die Detailwerte geben an, wie groß der Anteil des jeweiligen Haar-Wavelets am Gesamtsignal ist.

Die Approximationswerte approximieren das Signal in einer geringeren Frequenz. Vergleichen wir mit der Abbildung des ursprünglichen Signals, so gab es viel feinere Wellenberge. Visualisieren wir die Approximationswerte in der Box-Basis , so erhalten wir:

Es handelt sich also um eine gröbere, niederfrequentere Approximation der ursprünglichen Zeitreihe.

Auf dieser niederfrequenteren Approximation können wir nun erneut die diskrete Wavelet-Transformation mit unserem Low- und High-Pass-Filter anwenden. Wir erhalten:

Low-Pass (Approximationswerte)

• High-Pass (Detailwerte):

Mit den gefundenen Werten können wir jetzt mit den Basen und darstellen durch¹:

Sowohl die gröbste Box- als auch die gröbste Haar-Basis umspannen jetzt das gesamte Signal, weiter verfeinern können wir durch eine weitere Iteration also nicht mehr. Das Ergebnis der Wavelet-Transformation erhalten wir durch .

Dabei ist das grobe Restsignal, der Anteil des gröbsten Haar-Wavelets am Gesamtsignal und die Anteile der beiden feineren Haar-Wavelets am Gesamtsignal.

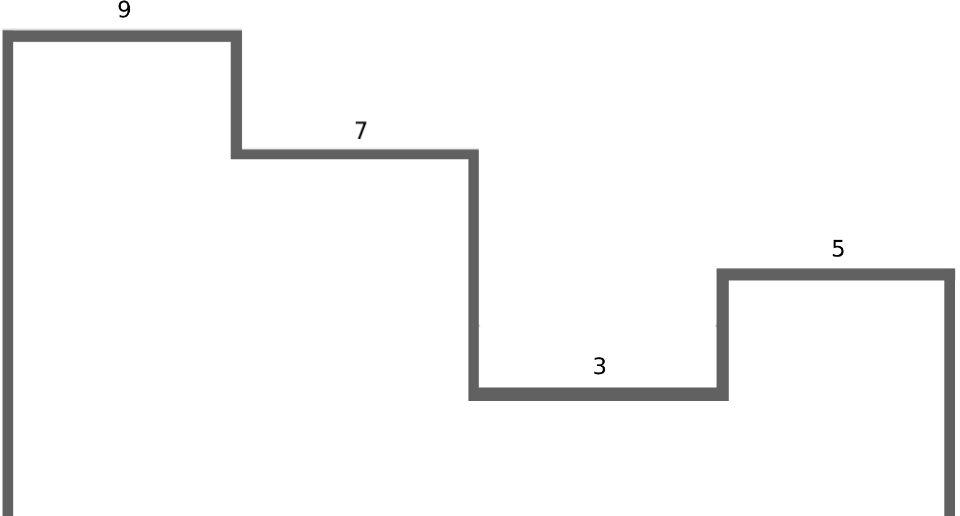
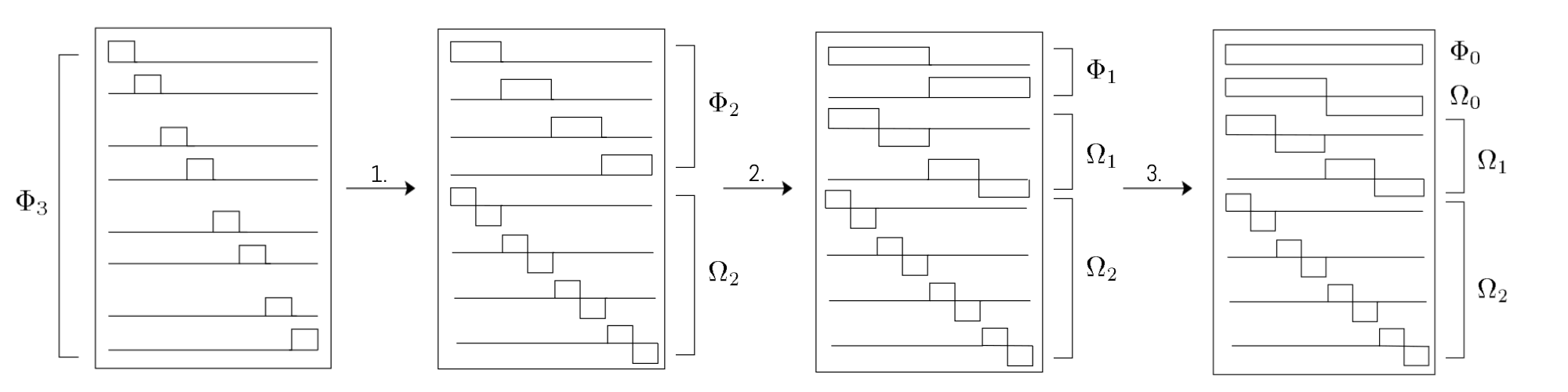
Hätten wir ein Signal mit statt Input-Werten gehabt, dann hätte das Vorgehen schematisch wie folgt ausgesehen³:

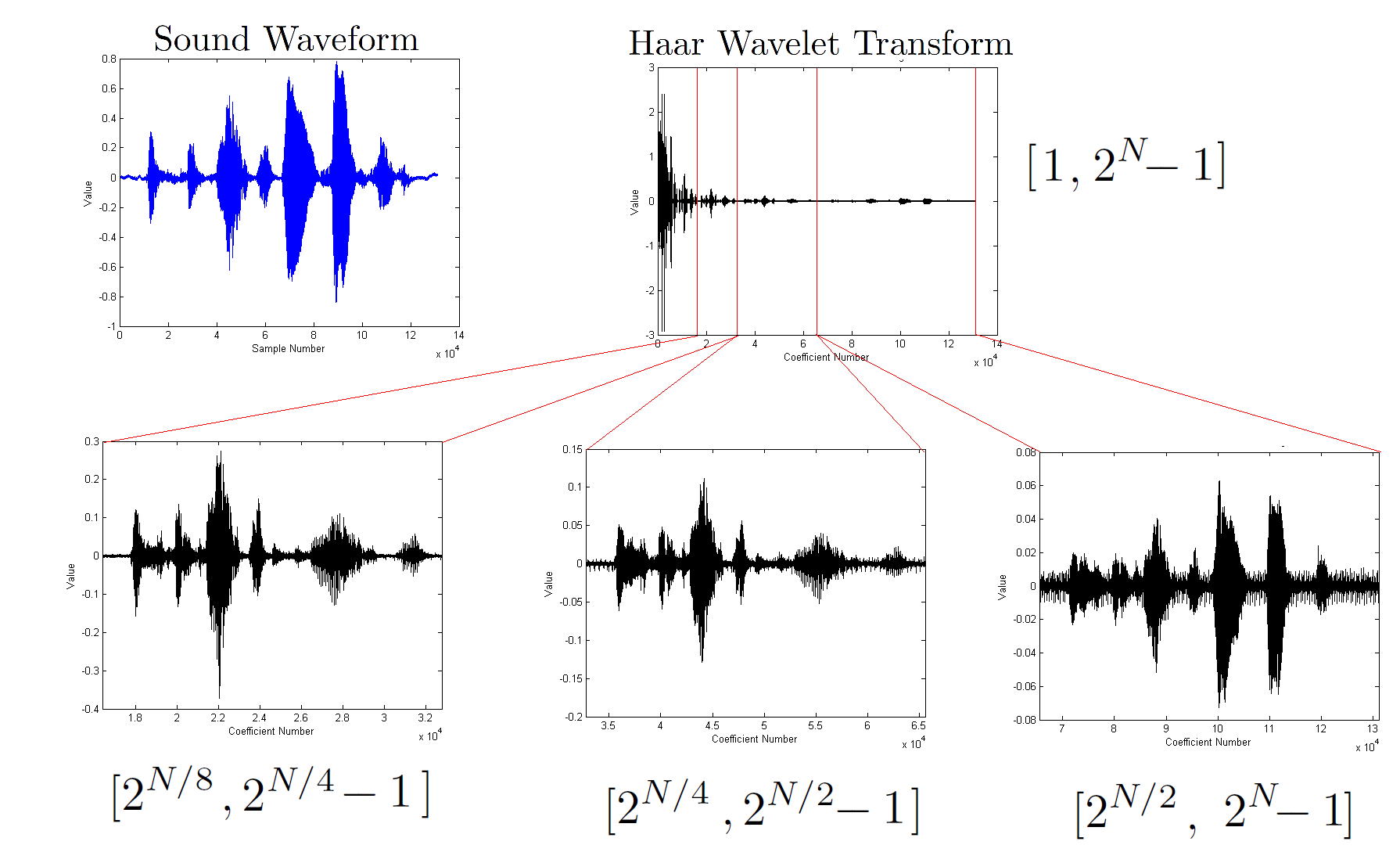
Dabei ist es normal, dass bei der Ausgabe der DWT die Koeffizienten verschiedener Wavelet-Größen hintereinander geschrieben werden. Wenn wir eine DWT plotten, können wir sehen, dass sich Ursprungssignal in mehreren Wavelet-Auflösungen wiederfinden lässt.

Hier in der rechten Hälfte , dem davorkommenden Viertel und dem davorliegenden Achtel )⁴:

Footnotes

1. übernommen von @owens1997 (Lecture #2, p. 8 ff.) ↩ ↩² ↩³ ↩⁴ ↩⁵

2. @owens1997 (Lecture #2, p. 5, Fig. 3 und 4) ↩

3. übernommen von @owens1997 (Lecture #2, p. 7, Fig. 5) ↩

4. Haar DWT of the Sound Waveform “I Love Wavelets”, Ctralie ↩