Definition - Weg in einem Graphen

• Konstrukte:
  • Kantendisjunkter Weg
  • Abstand zweier Knoten
  • Exzentrizität eines Knotens
• Generalisierungen:
  • Spaziergang (jeder Weg ist auch ein Spaziergang)
  • Teilgraph
  • Weg
• Hinreichende Aussagen:
  • Es gibt genau dann einen --Weg in , wenn es einen --Spaziergang in gibt.
• Involvierte Definitionen:
  • Weg
  • Graph
  • Teilgraph
• Veranstaltung: AlMa
• Referenz: @herzogWiSe22

⠀

Definition: Weg in einem Graphen

Sei ein Graph.

Den Teilgraphen bezeichnen wir als v-v’-Weg in , wenn er

• bei dem Knoten startet,
• bei endet,
• nur vorhandene Kanten “durchschreitet”
• und keinen Knoten zweimal passiert.

Die Länge des Weges ist gleich der Anzahl durchschrittener Kanten.

Anmerkung

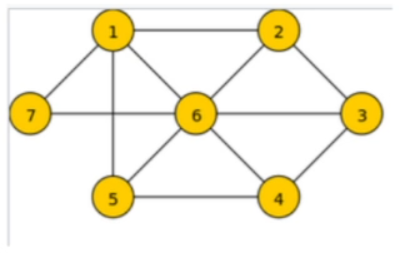
Beispiel

Sei folgender Graph gegeben:

Dann ist

• ein Weg mit Länge .
• kein Weg, weil es keine Kante zwischen und gibt.