Definition - Self-Attention

• Konstrukte:
  • Transformer
  • Multi-Head-Self-Attention
• Generalisierungen:
  • Neural-Network Layer
• Involvierte Definitionen:
  • Embedding
• Veranstaltung: EML
• Referenz: @sanderson2024a, @sanderson2024

⠀

Definition: Self-Attention

Als Self-Attention bezeichnen wir einen Layer-Typen neuronaler Netze, der dazu dient, Beziehungen zwischen verschiedenen Teilen einer Sequenz zu modellieren, wobei jeder Teil seine eigenen Gewichtungen in Bezug auf die anderen Teile berechnet.

Diese Beziehung wird in der Regel durch einen hochdimensionalen Output-Vektor repräsentiert.

Durch die hohe Dimensionalität ist der Output-Vektor in der Lage vielschichtige, komplexe Beziehungen zu modellieren: als (fiktionales) Beispiel das Konzept eines Miniatur Eiffelturm-Schlüsselanhängers aus Metall in der Hand einer Frau.

Die Funktionsweise eines Self-Attention-Heads lässt sich wie folgt herunterbrechen:

• Der Head erhält eine Reihe von Embeddings als Input.
• Für jedes Embedding werden Query-, Key- und Value-Vektoren berechnet.
• Für jedes Embedding wird die Relevanz der anderen Embeddings für das Embedding bestimmt, indem das Skalarprodukt aus Query und Key gebildet wird. Also: .
• Das Update des Embeddings , wird auf Basis der berechneten Relevanz des -ten Embeddings und Value-Vektors aktualisiert: .
• Der neue Embedding Vektor ergibt sich als Summe des ursprünglichen Embeddings und der Updates:

Definition: Query-Vektor

Als Query-Vektor des -ten Tokens bezeichnen wir einen Vektor, der genutzt wird, um die Relevanz der anderen Tokens in Bezug auf den -ten Token zu bestimmen.

Sei die lernbare Query-Matrix.
Sei der Embedding-Vektor des -ten Tokens.

Dann erhalten wir durch die Matrix-Vektor-Multiplikation

Definition: Key-Vektor

Als Key-Vektor des -ten Tokens bezeichnen wir einen Vektor, der genutzt wird, um die Relevanz des aktuellen Tokens in Bezug auf alle anderen Tokens zu bestimmen.

Sei die lernbare Key-Matrix.
Sei der Embedding-Vektor des -ten Tokens.

Dann erhalten wir durch die Matrix-Vektor-Multiplikation

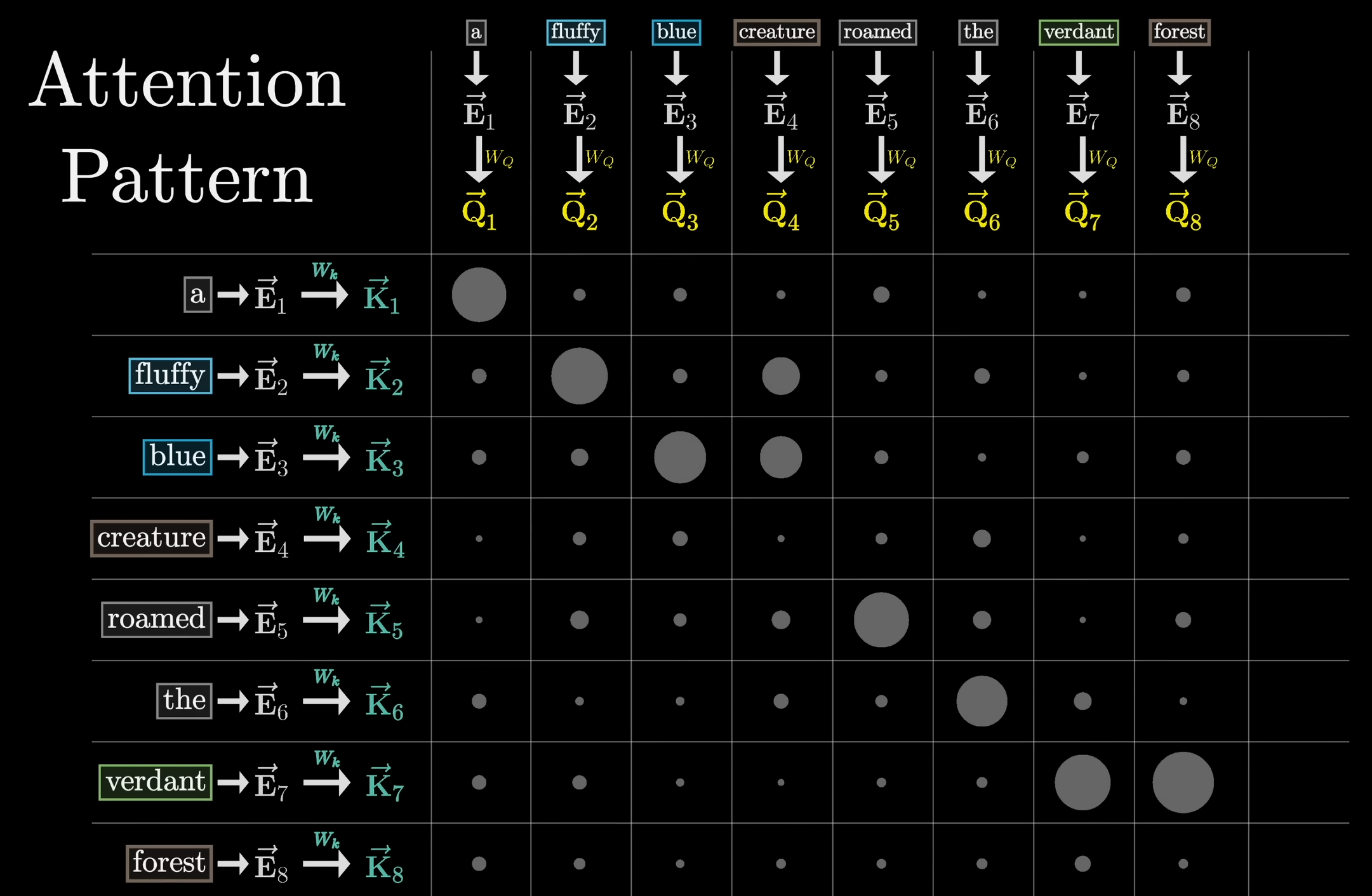
Relevanz als Skalarprodukt aus Query und Key

Sei der Index eines Tokens mit Query-Vektor
Sei der Index eines Tokens mit Key-Vektor .

Die Relevanz des Tokens auf den Token erhalten wir durch das Skalarprodukt

Semantisch können wir Query und Key so verstehen, dass die Query “eine Frage stellt” (als fiktionales Beispiel: bist du ein Adjektiv?) und der Key auf die Frage “antwortet” (in dem Beispiel: ja, ich bin ein Adjektiv).

Nach den Eigenschaften des Skalarproduktes gilt:

• ist groß, wenn die Vektoren in dieselbe Richtung zeigen.
• ist negativ, wenn die Vektoren in entgegengesetzte Richtungen zeigen.
• ist Null, wenn die Vektoren orthogonal zueinander sind.

Ist groß, so sagen wir, dass auf “attendet”.

Softmax-Relevanz und Stabilität

Um im Sinne einer Wahrscheinlichkeitsverteilung zu bestimmen, welche Tokens für eine Query am wichtigsten sind, wird auf den Vektor

abschließend noch eine (Temperature-)Softmax-Transformation angewandt.

Außerdem wird das Skalarprodukt von Query und Key im Sinne der numerischen Stabilität noch einmal durch die Wurzel der Dimension der Query/Key-Matrizen geteilt (denn wenn wir im Skalarprodukt sehr, sehr viele Werte zusammenaddieren, kann das Ergebnis ja auch ziemlich groß werden).

Definition: Attention Pattern

Berechnen wir die Query-Key-Skalarprodukt für alle Tokens und stellen das Ergebnis als Matrix dar, erhalten wir das Attention Pattern:

Die Größe des Attention Patterns entspricht dem Quadrat der Context-Size des Transformers, denn jeder Token des Inputs wird mit jedem anderen Token des Inputs in Verbindung gesetzt.

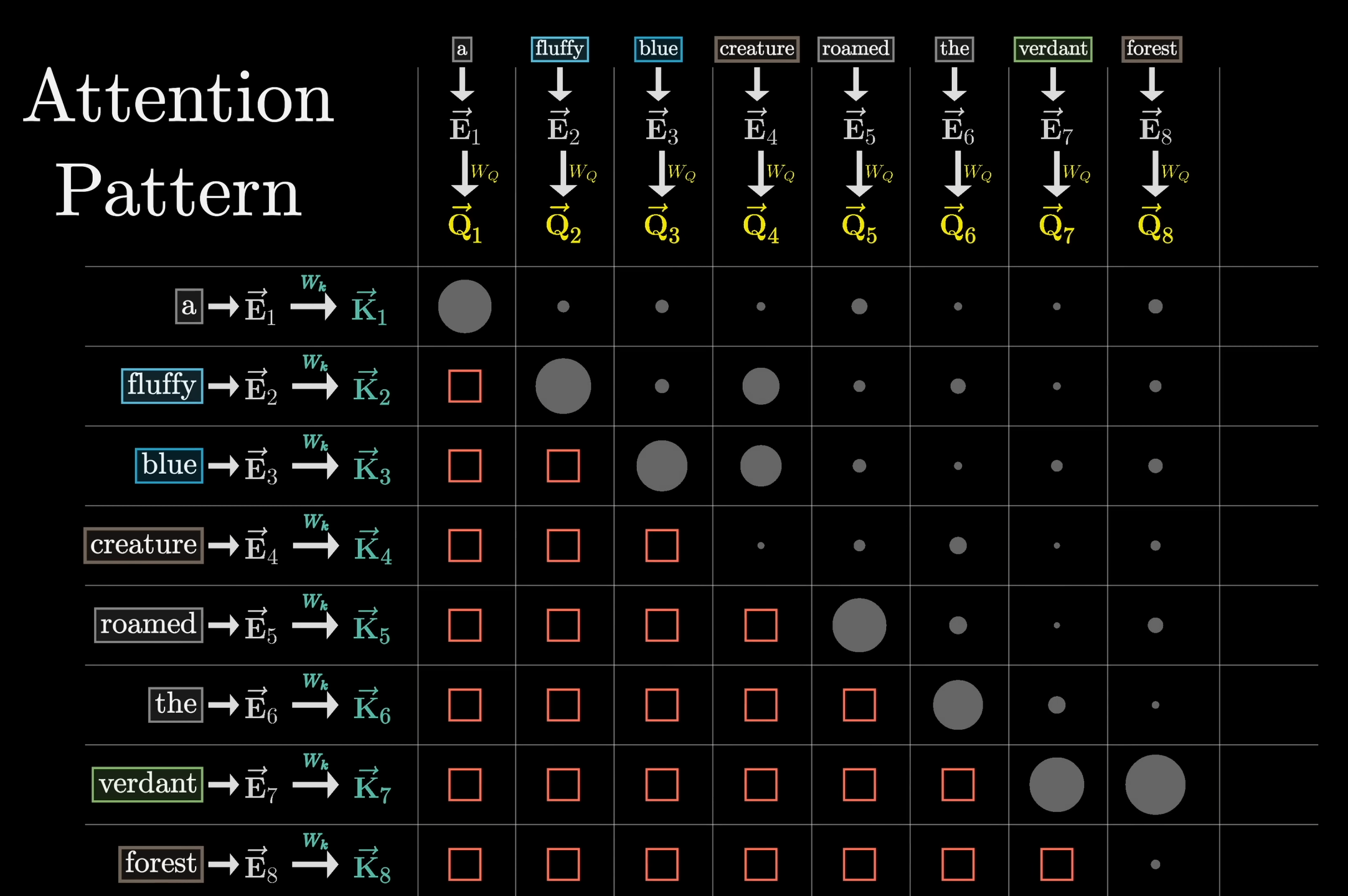
Definition: Masking

Beim Masking (auch Masked-Attention-Pattern) werden Tokens, die sequentiell gesehen nach dem aktuellen Token auftreten innerhalb des Attention-Patterns auf Null gesetzt ( vor der Softmax):

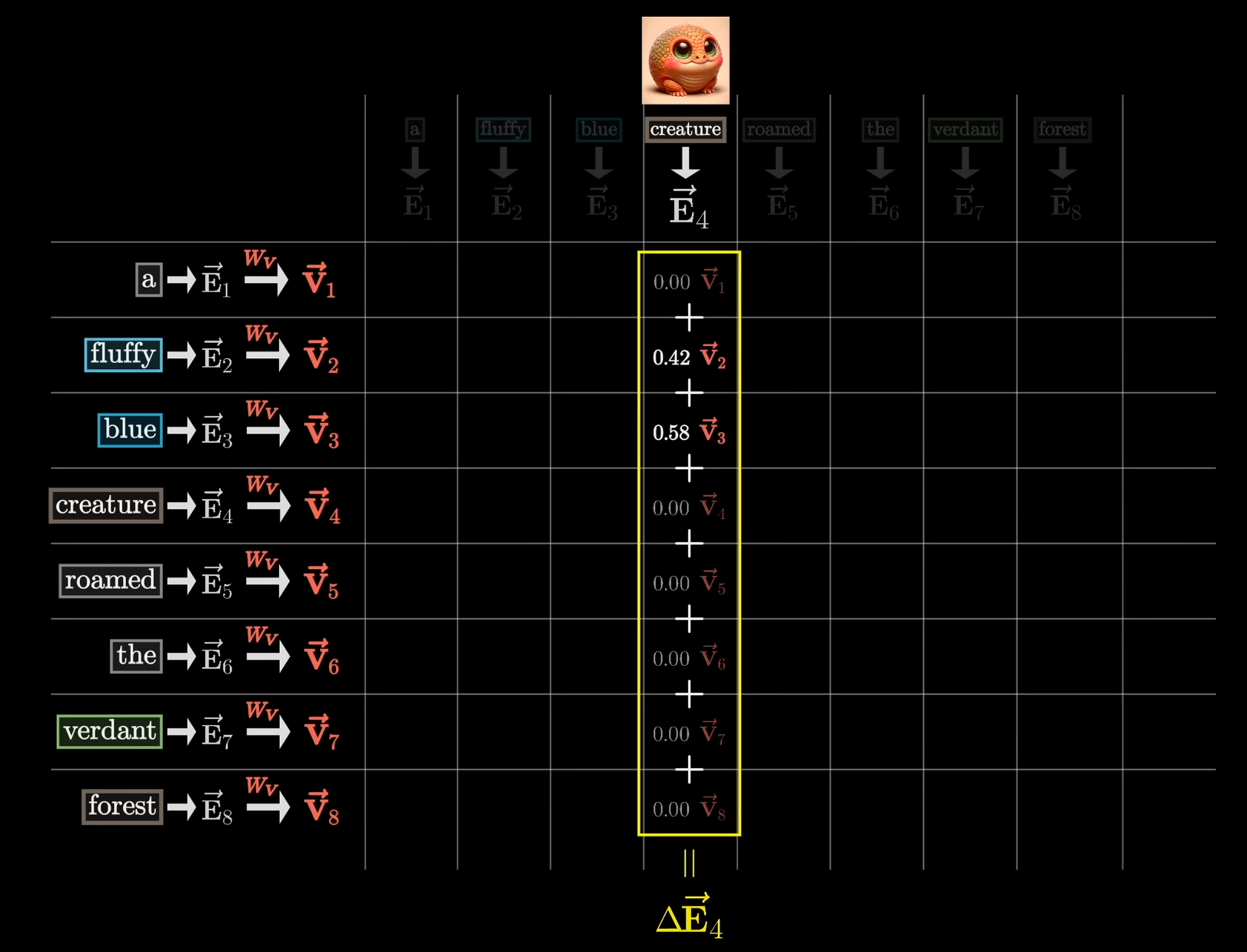
Aktualisierung des Embedding-Vektors auf Basis von Key, Query und Value-Matrix

Sei der Index eines Tokens mit Embedding-Vektor und Query-Vektor
Sei der Index eines Tokens mit Embedding-Vektor und Key-Vektor .

Um das Embedding von nun mit dem Kontext von zu aktualisieren, nutzen wir die sogenannte (ebenfalls lernbare) Value-Matrix und den Value-Vektor , wobei

Das Update des Embeddings durch das Embedding erhalten wir schließlich durch

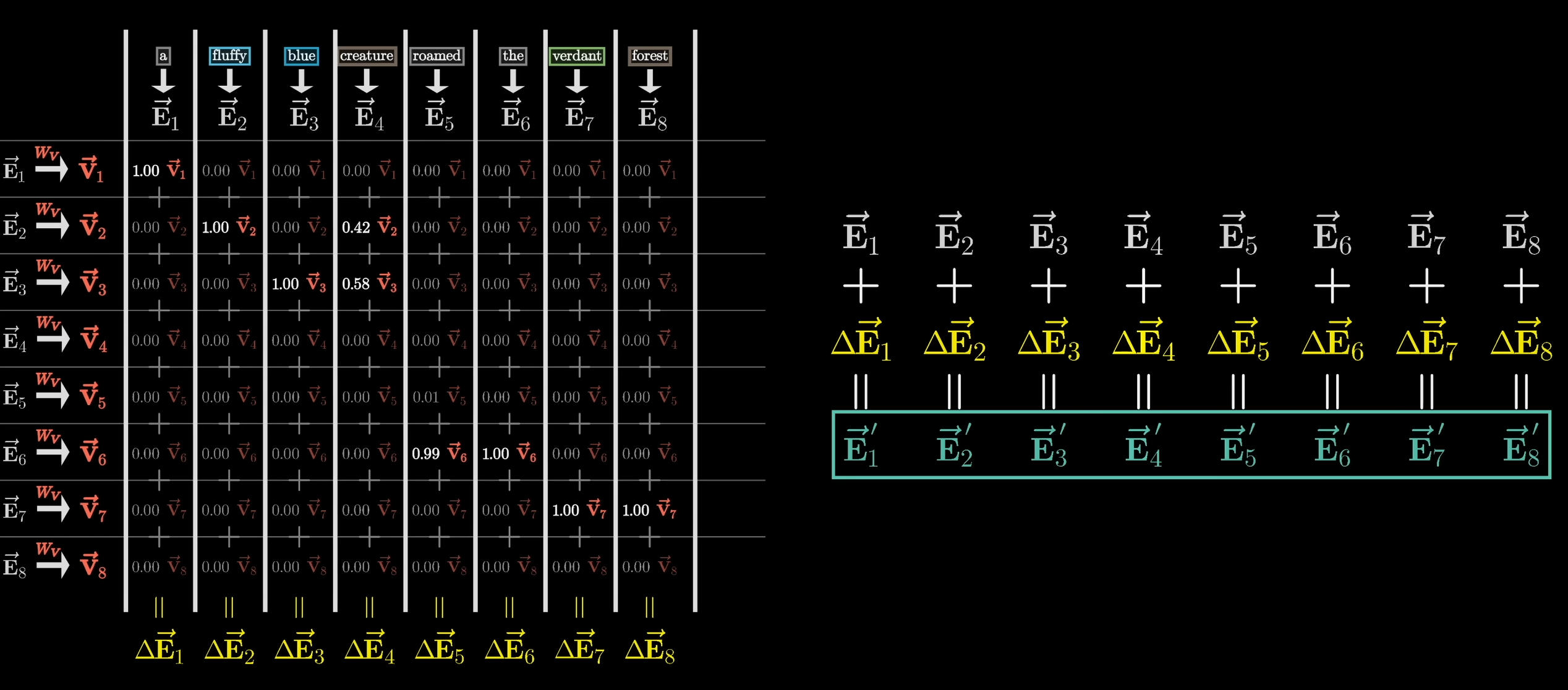
Aktualisierung des Embedding-Vektors auf Basis des Attention-Patterns

Sei die -te Spalte des Attention-Patterns.
Sei die Matrix aller Value-Vektoren, also

So erhalten wir das gesamte Update durch das Matrix-Vektor-Produkt

Den neuen Embedding Vektor erhalten wir schließlich durch

Dieses Update wird entsprechend für alle Embedding-Vektoren durchgeführt: