Involvierte Definitionen:Veranstaltung: DMReferenz: @valdes2025 (p. 248 ff.)
⠀
Proposition: Ausreißererkennung in Markovketten
Sei
ein endliches Alphabet.
Seidie Ordnung der Markovkette.
Seieine diskrete Folge über , die die Markoveigenschaft erfüllt. Als punktuellen Ausreißer bezeichnen wir das Folgenglied
(mit ), falls für einen vorgegebenen, anwendungsabhängigen Schwellwert
.
Anmerkung
Beispiel: Ausreißererkennung in einer Markovkette 1ter und 2ter Ordnung
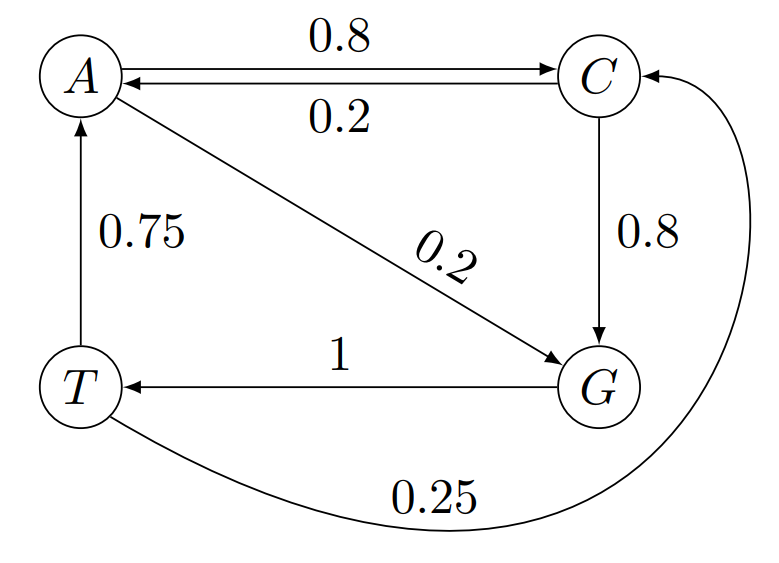
Die folgenden Abbildung zeigen eine Markovkette
-ter sowie -ter Ordnung über dem generischen Alphabet . Die korrespondierende diskrete Folge ist gegeben durch
Die zugehörige Markovkette erster Ordnung erhalten wir durch:
Wir untersuchen sie zunächst auf Anomalien. Sei der Schwellwert gegeben durch
. Als Ausreißer erhalten wir die Übergänge:
mit mit mit
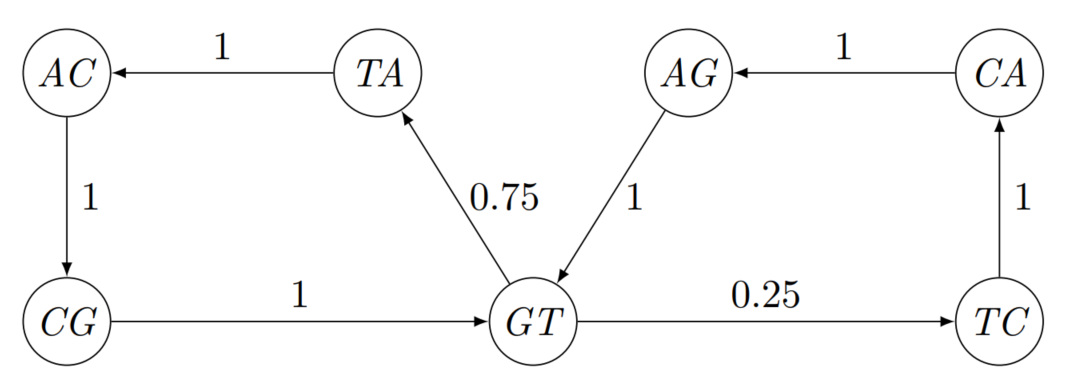
Die zugehörige Markovkette zweiter Ordnung erhalten wir durch:
Wir untersuchen nun auch die Markovkette zweiter Ordnung auf Anomalien.
Als Ausreißer erhalten wir lediglich den Übergang:
mit
Betrachtet man die diskrete Folge
erkennt man den folgenden Aufbau:
- ACGT …
- … CAGT …
- … ACGT …
- … ACGT
Hier sticht vor allem der zweite Block (CAGT) heraus. Es wird klar, dass der Übergang
nur eine Korrektur des fehlerhaften Übergangs darstellt. Daher ist das Ergebnis der Markovkette zweiter Ordnung plausibler. Als Ausreißer markieren wir daher: